
 | Computer Modeling in Engineering & Sciences |  |
DOI: 10.32604/cmes.2021.015314
ARTICLE
A Homogeneous Cloud Task Distribution Method Based on an Improved Leapfrog Algorithm
1School of Mechanical Engineering, Sichuan University, Chengdu, 610065, China
2Chengdu Yigao Intelligent Technology Co., Ltd., Chengdu, 610065, China
*Corresponding Author: Ji Xiong. Email: 13668149296@163.com
Received: 08 December 2020; Accepted: 08 April 2021
Abstract: Cloud manufacturing is a new manufacturing model with crowd-sourcing characteristics, where a cloud alliance composed of multiple enterprises, completes tasks that a single enterprise cannot accomplish by itself. However, compared with heterogeneous cloud tasks, there are relatively few studies on cloud alliance formation for homogeneous tasks. To bridge this gap, a novel method is presented in this paper. First, a homogeneous cloud task distribution model under cloud environment was constructed, where services description, selection and combination were modeled. An improved leapfrog algorithm for cloud task distribution (ILA-CTD) was designed to solve the proposed model. Different from the current alternatives, the initialization operator and the leapfrog operator in ILA-CTD can ensure that the algorithm always searches the optimal solution in the feasible space. Finally, the processing of task allocation for 1000 pieces of medical labeling machine bottom plates was studied as a case to show the feasibility of the proposed method. The superiority of ILA-CTD was also proven based on more optimal solutions found, compared with the three other methods.
Keywords: Cloud manufacturing; service composition; tasks distribution; intelligent optimization; leapfrog algorithm
The application of modern technologies (the Internet of Things [1,2], service-oriented technology [3], cloud computing [4], big data [5], etc.) had a profound impact on manufacturing methods. Cloud manufacturing (CMfg) is a network-based and knowledge-enhanced manufacturing model, it is a specific form of the service-oriented manufacturing paradigm [6]. Generally, there are two types of clouds: private clouds in large enterprises [6,7] and public clouds for small and medium enterprises (SMEs) [8]. The application of CMfg in SMEs would better reflect the characteristics of CMfg, such as centralized management of distributed resources, crowd-sourcing manufacturing, and highly shared manufacturing resources [9].
There is consistent requirement in CMfg in SMEs, namely that a large order needs to be fulfilled in a short time, this is undertaken by an alliance of multiple SMEs [10]. A single SME is unable to complete such a large order in a timely manner. A reasonable distribution of a large order to multiple SMEs can drastically reduce the time required to fulfill the order, because the order can be executed parallelly. The global optimization for this activity can be achieved through reasonable task allocation according to the capabilities of the alliance members. Two crucial steps are needed to form a cloud alliance: selection of members (services selection) and reasonable task distribution (services composition) [11].
Selection of alliance members, namely services selection (SS) can be achieved through methods such as semantic similarity [12], QoS (quality of services) [13] and rough-fuzzy approach [14]. For task distribution, cloud manufacturing relates to two types: heterogeneous tasks that require different services [15], and homogeneous tasks that require the same services [16]. The difference is that the latter selects services based only on QoS, and even if the production capacity of an individual service is insufficient, a large number of available services will still be obtained. However, not every available service can be assigned a task because there is the constraint of starting quantity. Therefore, how to reasonably allocate mass homogeneous tasks to such services is a complicated question with many constraints such as production capacity, QoS, and starting quantity. To propose a solution to this problem, an improved leapfrog algorithm for cloud task distribution (ILA-CTD) is presented in this study. A novel initialization operator was designed in this method to avoid the solution modification caused by the restriction of the starting quantity. The solution obtained by the leap operator satisfies the restriction of the starting quantity. Pareto optimal theory was applied to leapfrog algorithm, so that the proposed algorithm has the ability to deal with multi-objective optimization problems.
This article is organized as follows: Section 2 reviews related works; Section 3 presents the proposed model; Section 4 introduces the novel task distribution method; Section 5 describes a case study with the results discussions; and Section 6 concludes the study with remarks and suggestions for future work.
Manufacturing services are usually designed to be user-friendly (i.e., services can be easily identified through accurate description of QoS). After alternative services are found, discrimination of the services with overlapping or identical functionalities based on QoS can be achieved [17,18]. However, things become more complex when a task consists of several subtasks, that need multiple services to accomplish collaboratively [16].
Many methods have been developed to rank and select services. Zhao et al. [19] proposed an optimal service selection approach using crowd-based cooperative computing, whose main contribution was optimally balancing the QoS and the synergy effect. Eisa et al. [18] presented a Multi-Criteria Decision-Making model to rank services based on various QoS attributes; unlike other approaches, their work was based on a real cloud provider (Amazon). Hussain et al. [20] presented a novel customer-centric Methodology for Optimal Service Selection (MOSS) in a cloud environment. Bouzary et al. [21] used TF-IDF (term frequency-inverse document frequency) to identify services that satisfy QoS. A modified interval DEA model with undesirable outputs has been adopted to achieve more accurate web service selection [22]. In addition, the dynamic change of consumer requirements was also considered by Devi et al. [23], they proposed a Linear Programming model to rank and select services dynamically.
Obviously, QoS plays an important role in cloud services selection. To build upon previous research, a selection method for homogeneous services based on QoS is proposed in this work.
2.2 Task Distribution and Services Composition
From ants to human beings, animals have the ability to cooperate, communicate and divide labor among individuals, which is inspiring collaborative manufacturing. Chen et al. [16] proposed an improved multi-objective evolutionary algorithm based on the decomposition-particle swarm optimization (MOEA/D-PSO) to obtain the optimal combination of services. Aimed at minimizing the making span, monetary and energy costs of tasks in the cloud-fog paradigm, a two-tier bipartite graph task allocation approach was presented by Gad-Elrab et al. [24] based on fuzzy set theory. Gigliotta et al. [25] examined the issues in task allocation in homogeneous communicating robots using the evolutionary algorithm. Sharma et al. [26] proposed an improved cloud task allocation strategy using a modified K-means clustering technique. A hybrid approach combining the features of genetic algorithm and the analytical hierarchy process, was implemented by Mostafa et al. [27] to distribute tasks to service suppliers. A multi-objective genetic algorithm was used by Jiang et al. [28] to allocate the disassembly tasks in the cloud environment. Jatoth et al. [29] presented an Optimal Fitness Aware Cloud Service Composition (OFASC) to balance multiple parameters of QoS. Zhou et al. [30] used evolutionary algorithms for many-objective cloud services composition. Somasundaram et al. [31] designed and developed a cloud resources broker (CLOUDRB), which integrated CLOUDRB with deadline-based job scheduling. They also developed a particle swarm optimization (PSO)-based resource allocation mechanism, to allocate users’ requirements to cloud resources in a near-optimal manner.
In summary, task distribution (services combination) is a complex problem, and intelligent evolution algorithms (such as GA, EA and PSO) have made substantial contribution to address the complexities. Inspired by the previous efforts, ILA-CTD is proposed in this study to address the homogeneous cloud task distribution problem.
3 Homogeneous Task Distribution Model
The manufacturing resources in CMfg are encapsulated as manufacturing service in a cloud resources pool. When the manufacturing tasks published in CMfg, three stages follow, namely, task decomposition, services selection, and services composition. The homogeneous cloud task distribution model is shown in Fig. 1.
Manufacturing resources of factories are virtualized to various cloud services in a cloud service pool. When the tasks are uploaded, the service pool will be searched and available services will be selected. Then, the optimal service combination will be determined to identify an optimized cloud manufacturing alliance. The factories in the alliance will be notified to perform manufacturing tasks. The focus of our work is services selection and combination optimization, specifically for homogeneous tasks. This is expressed in Eq. (1):
Tp(n) indicates cloud tasks with n products, Pj is the ith product; Sc(f) is the set of available services; Sj is the jth available service;
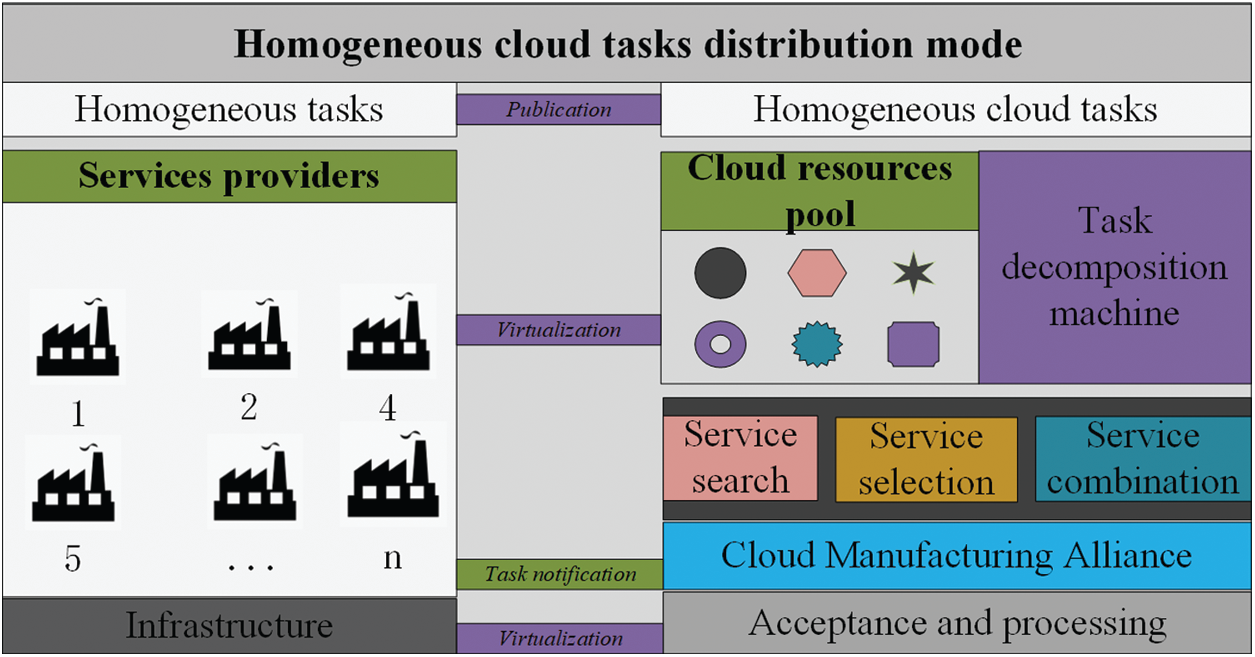
Figure 1: The model of homogeneous cloud task distribution
3.2 Service Description and Selection
3.2.1 Manufacturing Service Description in the Cloud
Offline services selection mainly focuses on QoS, which involves cost, time, and quality. However, for cloud services, the attributes that affect the quality of the cloud manufacturing alliance also need to be considered. Evaluation indexes proposed by Chen give a comprehensive description of cloud manufacturing services; cloud manufacturing services (C-QoS) were expressed as 6 tuples (C-QoS = {SI, G, C0, T, C, Q}) [16].
1) SI shown in Eq. (2) is the quality consistency:
SIi is the quality consistency of ith cloud alliance;
2) G shown in Eq. (3) is the composability:
Gi is the composability of the ith cloud alliance;
3) C0 shown in Eq. (4) is communication ability:
Coi is the communication ability of the ith cloud alliance;
4) T shown in Eq. (5) is the time consumed by service:
Ti is the consumed time of the ith cloud alliance;
5) C shown in Eq. (6) is the cost:
Ci is the cost of the ith cloud alliance;
6) Q shown in Eq. (7) is the quality:
For r candidate services in the cloud pool, incapable services should first be eliminated from selection. Then, f (
rk is the kth requirement, and ak is the value of the service attribute corresponding to rk.
The distribution model of n products to f available services is shown in Eqs. (9)–(11). As
Therefore, a complex problem arises, because product quantities undertaken by each service and different service combinations will constitute different cloud alliance options. We assign a reasonable quantity and
Tr and Cr represent consumer expectations of time and cost, respectively.
The leapfrog method is an efficient algorithm with both hereditary and group behavior [32–34]. However, the classic leapfrog algorithm is incapable of solving the above model because it is a multi-objective optimization problem, and many infeasible solutions will be generated because of the constraint of starting quality. To solve the presented model, an improved leapfrog algorithm for cloud task distribution (ILA-CTD) is proposed.
Pareto domination: Assuming that a and b are two solutions of a multi-objective function F with m benefit-oriented targets and n cost-oriented targets, if
Non-dominated solution: Assuming that c is a feasible solution of a multi-objective function F with m targets, if there is no other solution d that satisfies Fi(c)
Elite archives: Set of non-dominated solutions obtained in the process of searching for the best solution.
4.2.1 Initialization of Frog Population
A solution of the model is mapped to a frog Ui = (s
unidrnd(f) is a function that produces an integer from 0 to f; a and b are the initial speed factors; c is the diversity factor; and r is a random number between 0 and 1.
n is the total number required to be distributed. Obviously, all solutions obtained through the designed initialization method satisfy the constraint of starting quality, and the diversity of population P is also guaranteed via factor c.
A fitness function shown in Eq. (14) was designed to rank frogs, where fi is the fitness value of the ith frog in a population.
Dividing p frogs into q groups, where
The search process constantly makes the worst frog in each memeplex leap to a better position. The leap operator
Uw is the worst frog in a memeplex, and Ub is the best frog. It is easy to prove that the solution obtained via the leap operator also satisfies the constraint of starting quality, which is more efficient than the other methods that consume time to amend infeasible solutions.
Proof. If Ui = (s
Hence, Uw = Uw +(Ub − Uw) satisfies constraint that
Ub is feasible and satisfies the constraint of starting quality. Therefore,
Local search replaces the worst frog with a better one in each memeplex. The flowchart is shown in Fig. 2.
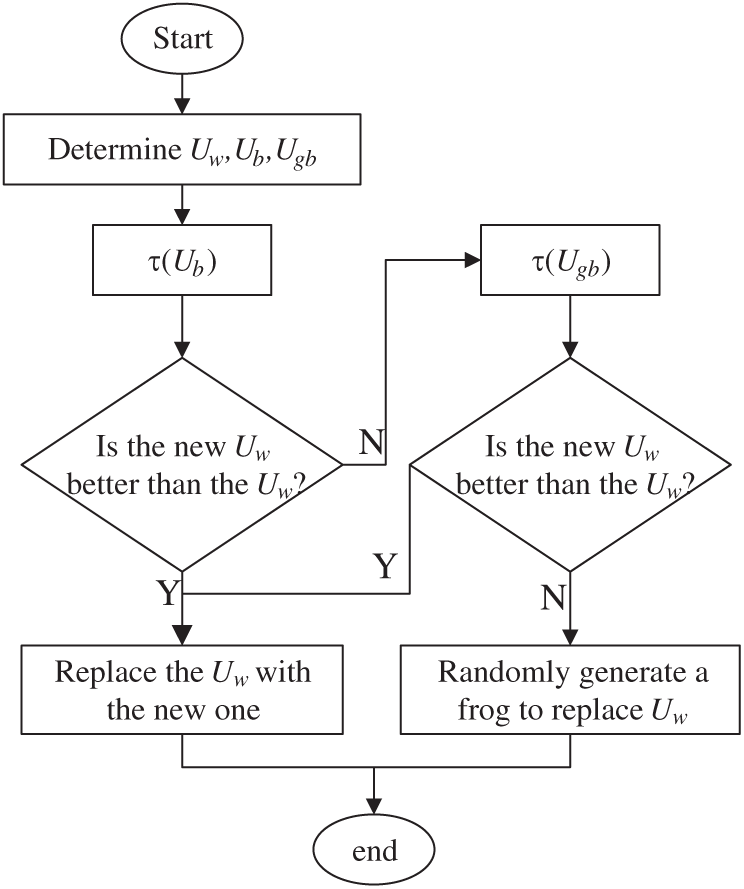
Figure 2: Flowchart of local search
Step 1: Find the local worst frog Uw, the local best frog Ub, and the global best frog Ugb.
Step 2: Update Uw by using the leap operator
Step 3: Is the new Uw better than the old one? If yes, go to Step 4; else, go to Step 5.
Step 4: Replace the Uw with the new one.
Step 5: Update the Uw by using the leap operator
Step 6: Is the new Uw better than the existing Uw? If yes, go to Step 4; else, go to Step 7.
Step 7: Randomly generate a frog to replace Uw.
Based on the above operators, the flowchart of ILA-CTD is shown in Fig. 3. The detailed steps are as follows:
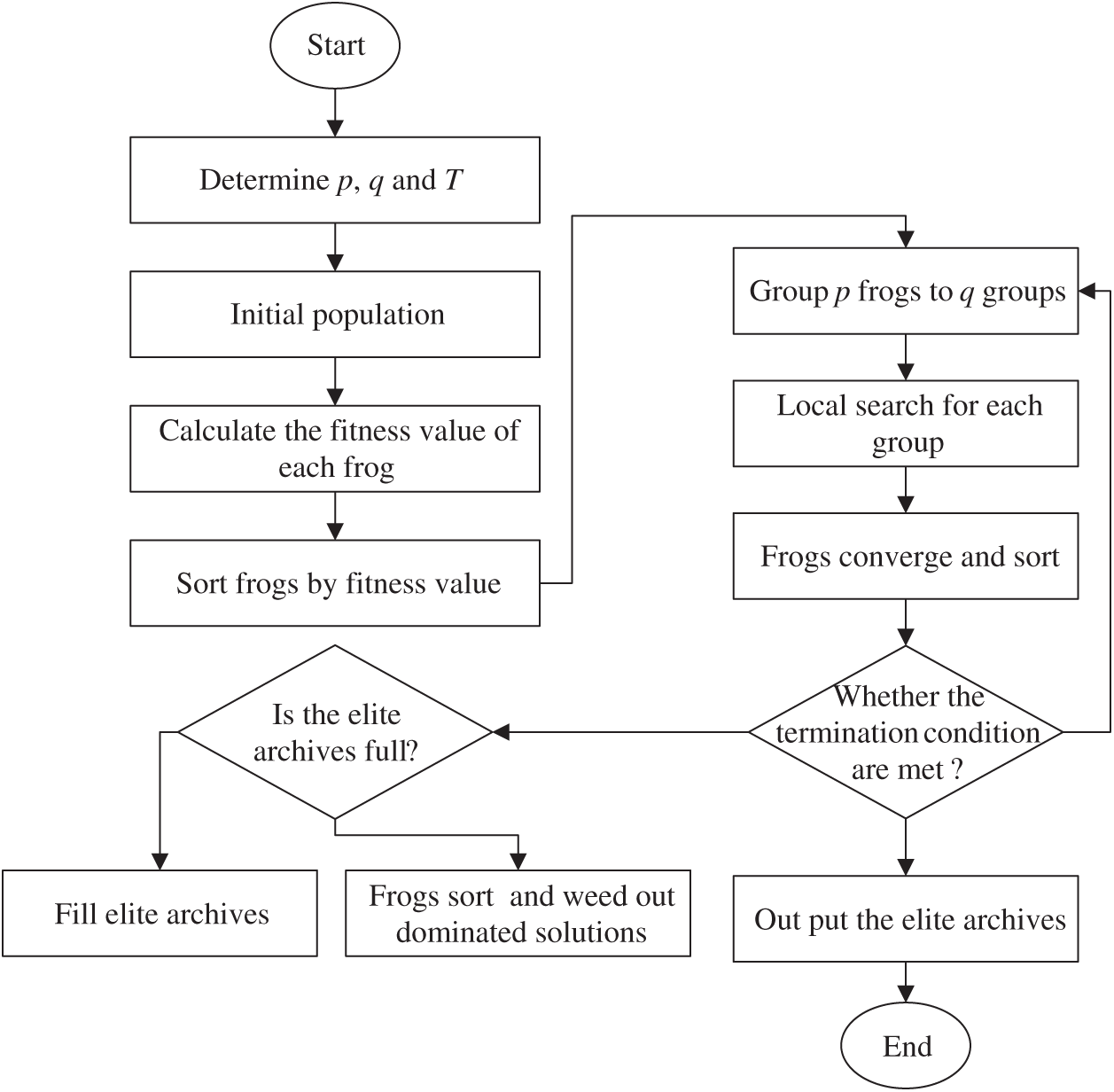
Figure 3: Flowchart of ILA-CTD
Step 1: Determine the population size p, number of group q, and termination condition T.
Step 2: Initialize population with the proposed method.
Step 3: Calculate the fitness value of each frog in the population.
Step 4: Sort frogs by fitness value.
Step 5: Group p frogs into q groups.
Step 6: Perform local search for each group (update the worst one in each group).
Step 7: Converge frogs in each group, and sort frogs by fitness value again.
Step 8: Whether termination condition is met? If yes, go to Step 9; else, go to Step 10.
Step 9: Are the elite archives full? If the elite archives are not full, then fill elite archives with non-dominated solutions obtained in this generation; else, discard dominated solutions in the elite archives and fill with non-dominated solutions. Then, go to Step 5.
Step 10: Out put the elite archives.
The allocation of processing 1,000 pieces of medical labeling machine bottom plates shown in Fig. 4, was used as a case to demonstrate the feasibility of the proposed method. The performance of the plate mainly depends on the dimensional accuracy Q1, position accuracy Q2 of the holes, and flatness Q3 of the plate. The specific accuracy requirements and delivery time constraint is shown in Tab. 1; 10 available services shown in Tab. 2 were obtained after services selection.
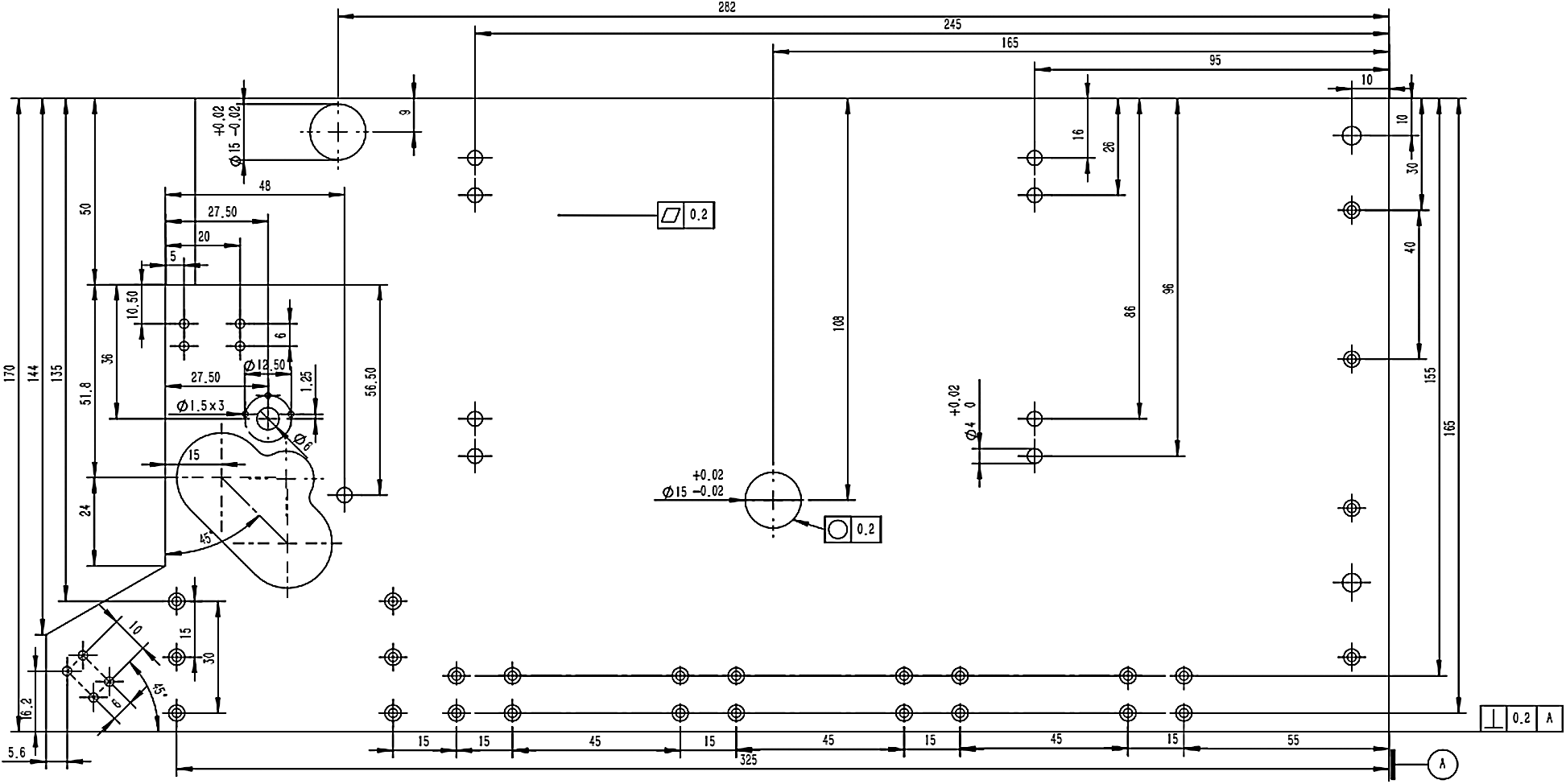
Figure 4: Medical labeling machine bottom plate

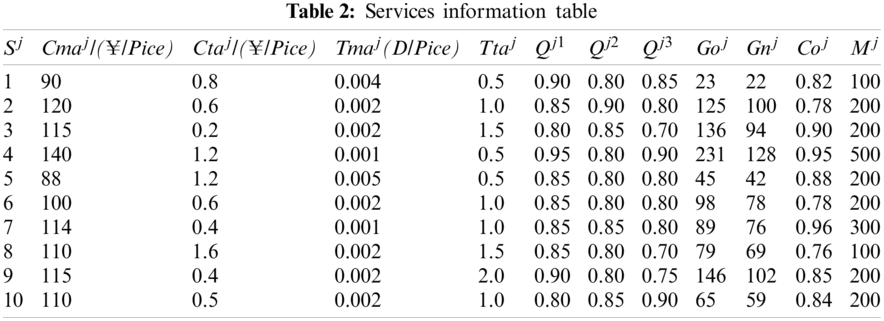
A personalized solution is always required in actual application, and a comprehensive evaluation based on consumer preferences for targets is necessary. Therefore, the function shown in Eq. (18) was adopted to normalize the attributes values.
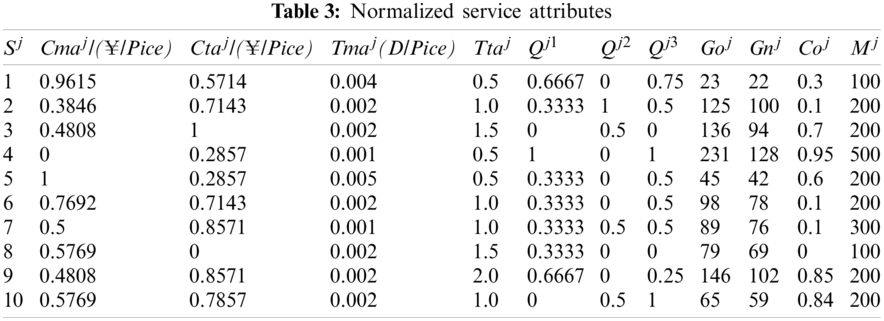
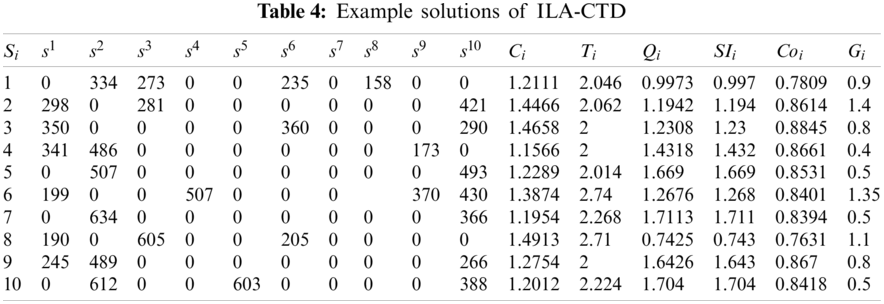
Then, the experiment was conducted under the environment of Windows10 and MATLAB 2016a. The parameters of ILA-CTD were set as population size
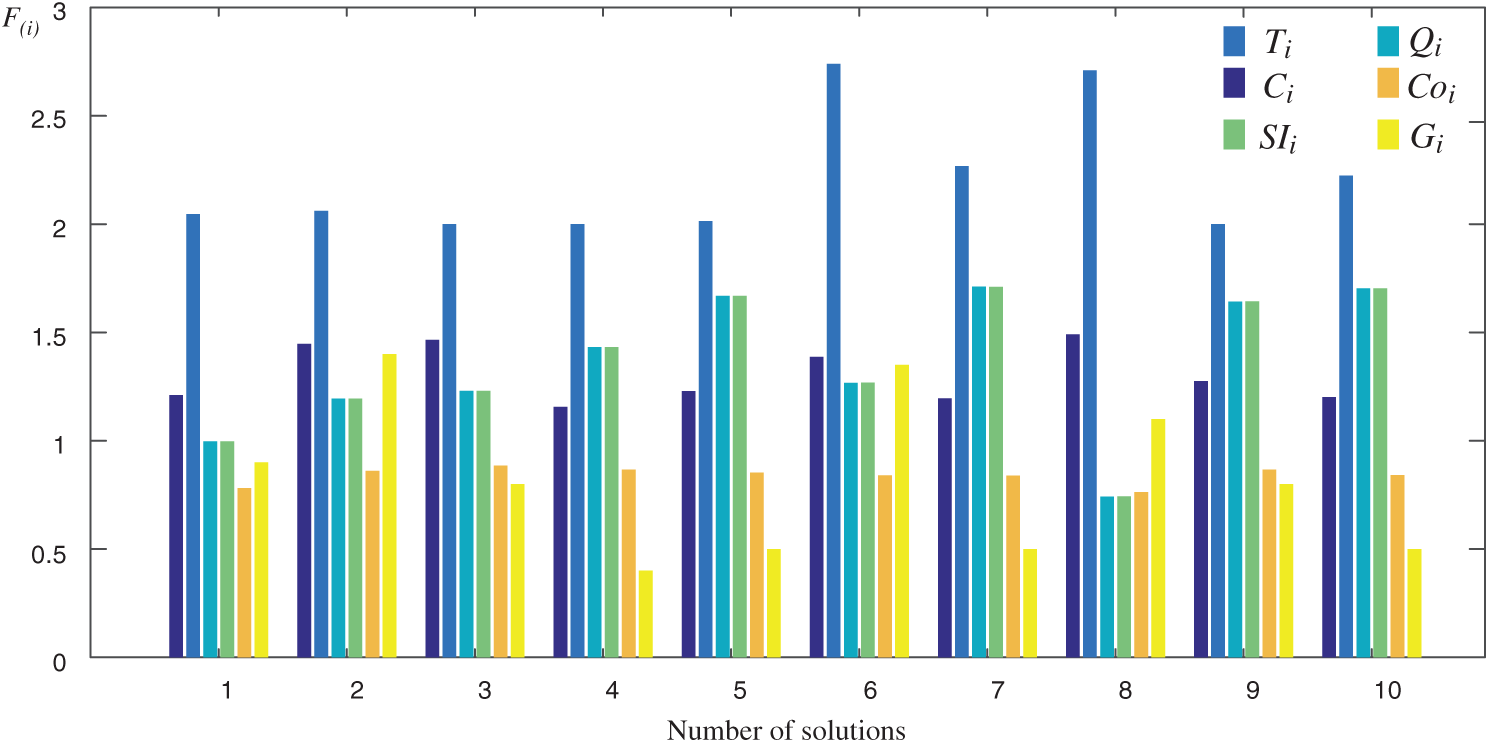
Figure 5: Performances of solutions obtained through ILA-CTD
The number of non-dominated solutions in the elite archives of each generation (
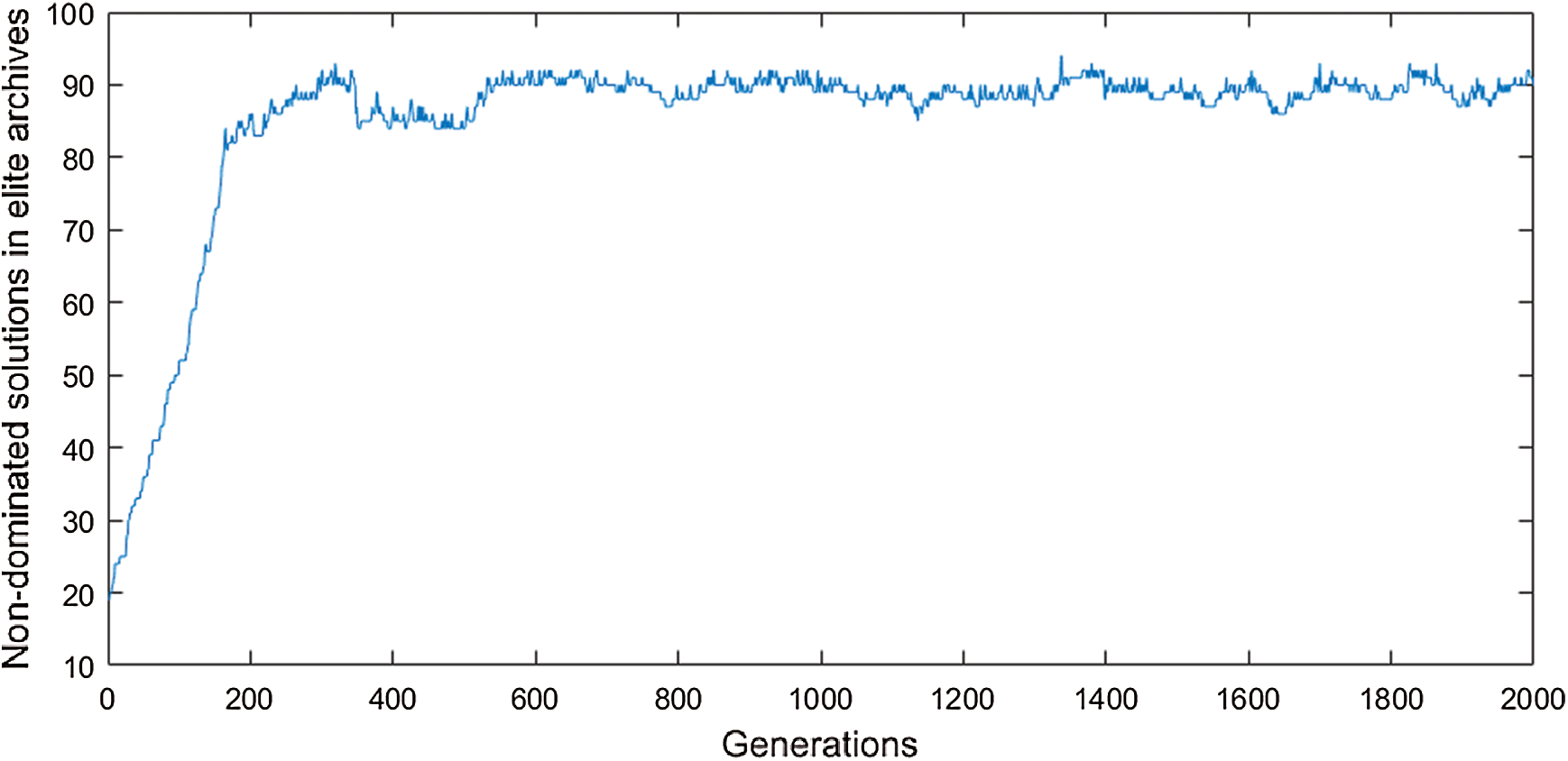
Figure 6: Non-dominated solutions in the elite archives of each generation
The IGD (inverted generational distance) is a simple way to evaluate the convergence of the algorithm based on the optimal solutions set. However, it is impossible for this problem. Because the optimal solutions cannot be obtained at first. Therefore, a new measure was constructed to evaluate the performance of the method proposed in this article. The model proposed in this work is a six-targets problem, and it is difficult to directly display the Pareto frontier. If the algorithm converges, then it means the Pareto frontier converges to a certain area. Thus, the average distance between adjacent generations should become steady. Hence, the average distance between adjacent generations (Da) was adopted to evaluate the convergence of the proposed method (Eq. (19)).
D(s*i, sj) is the distance between the ith solution in the kth generation and the jth solution in the (k + 1)th generation; n1 and n is the number of non-dominated solutions in the elite archives of the kth and the (k + 1)th generation, respectively. The evolution process of Da along generations is shown in Fig. 7.
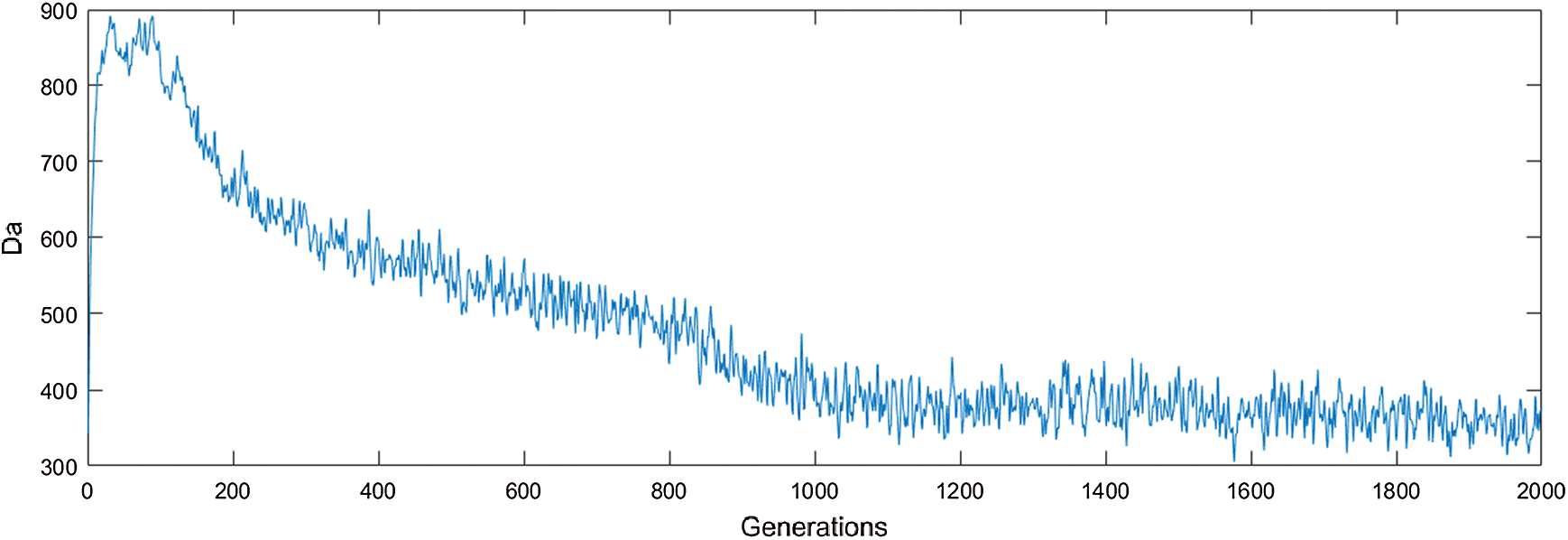
Figure 7: Average distance between adjacent generations
As shown in Fig. 7, Da rises sharply at first, then falls, and finally stabilizes, which is consistent with the process predicted by the algorithm. The phenomenon results because of three reasons: (1) The non-dominated solutions with different search directions increase dramatically as the generations increase, (2) the optimal search direction is determined progressively and the non-dominated solutions tend to the definite search direction; so, Da decrease, and (3) the Pareto frontier is found, Da becomes steady, which validates that the proposed method converges.
To assess the performance of the method proposed in this work, the results obtained via ILA-CTD were compared with MOEA/D-PSO, MOEA/D-GA [11], and NSGA-
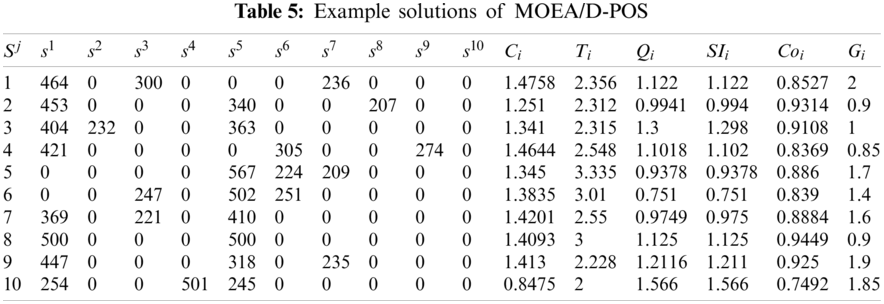
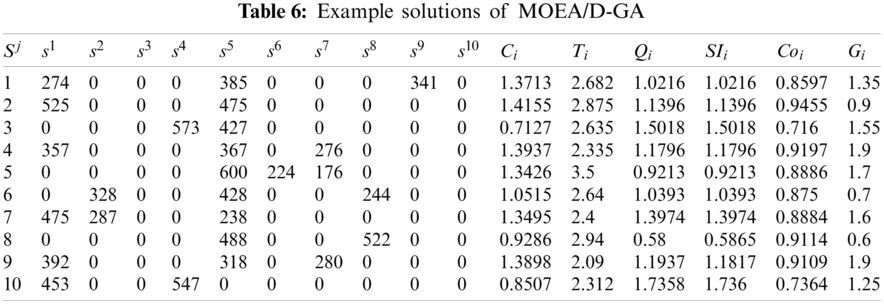
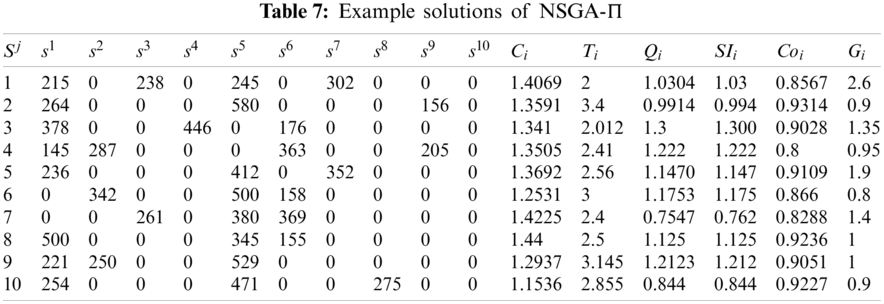

Figure 8: Performances of solutions obtained through MOEA/D-PSO

Figure 9: Performances of solutions obtained through MOEA/D-GA
Because MOEA/D-PSO, MOEA/D-GA, and NSGA-
1) Proportion of non-dominated solutions in mixed Pareto set ta
Selecting m solutions from each Pareto set that was finally obtained via MOEA/D-PSO, MOEA/D-GA, NSGA-
D(ma) is the number of non-dominated solutions obtained through method a (a
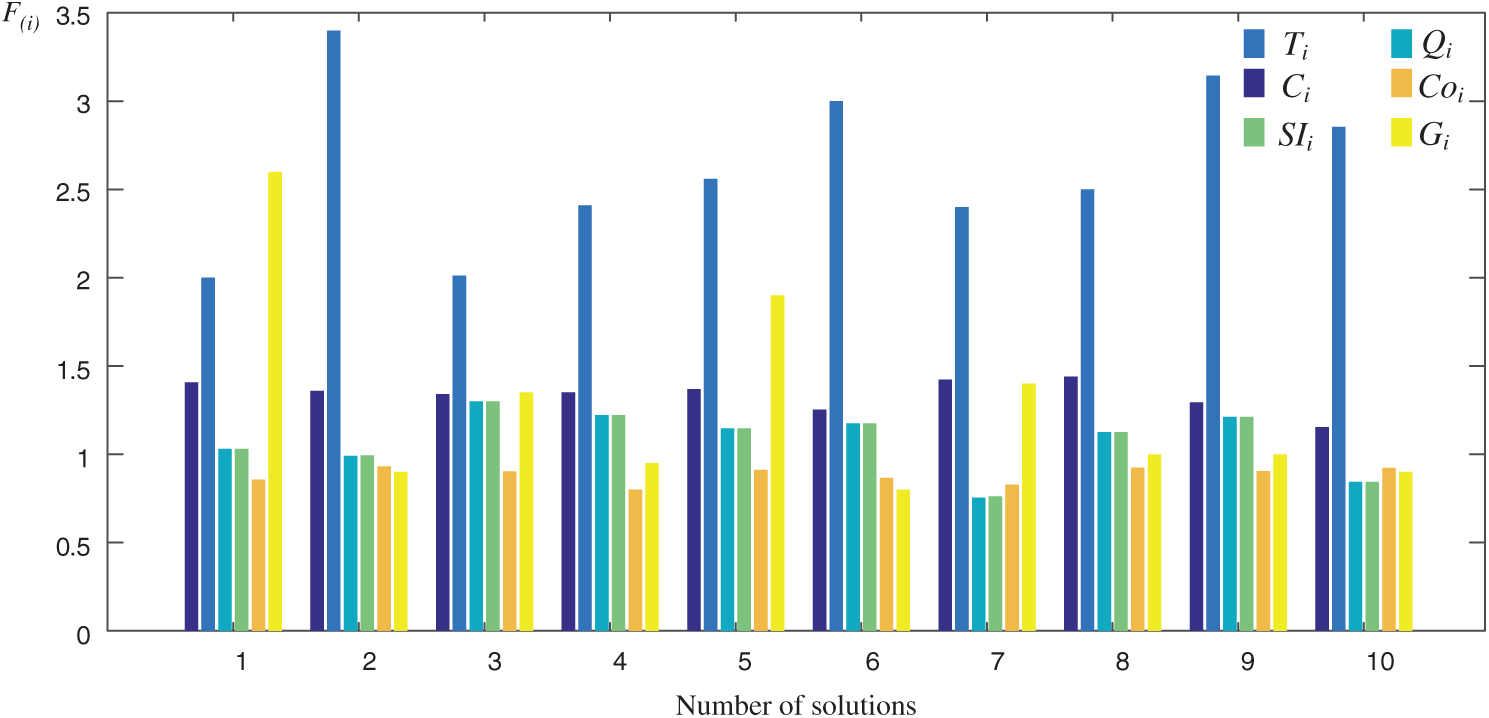
Figure 10: Performances of solutions obtained through NSGA-
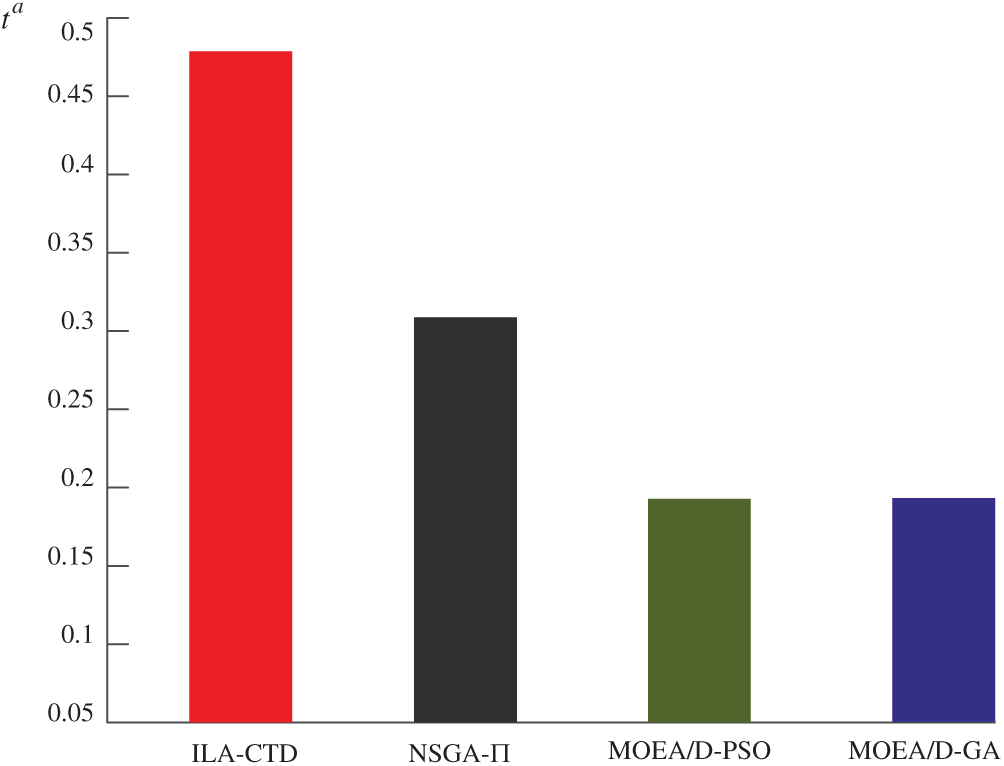
Figure 11: Performance of ILA-CTD in each generation
As the generations increased, more and more non-dominated solutions in PD were obtained via ILA-CTD. From the perspective of the number of non-dominated solutions in PD under the same conditions (T = 2000 and m = 10), ILA-CTD performed best, followed by NSGA-
2) Proportion of feasible solutions Pf
In practical applications, the obtained solutions must be feasible. Most evolutionary algorithms deal with infeasible solutions through a penalty function. The feasibility of all final solutions cannot be guaranteed if the penalty function is unreasonable; therefore, Pf can express the reliability and practicability of a method. The Pf of ILA-CTD, NSGA-
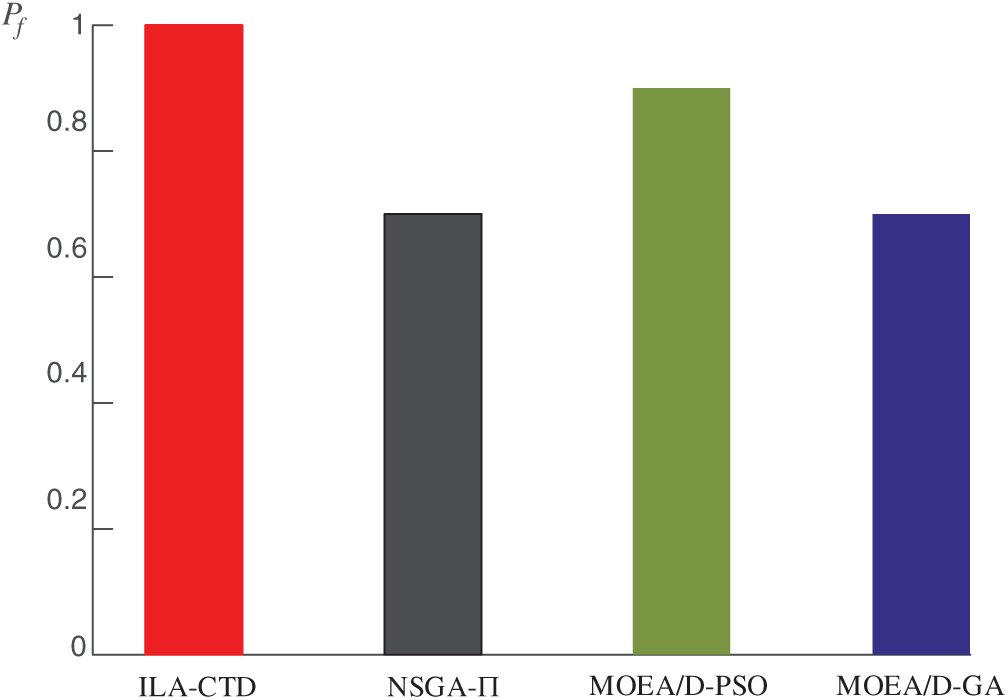
Figure 12: Pf of each method
From the perspective of Pf in the final output solutions, ILA-CTD performed best, followed by MOEA/D-PSO, NSGA-
As one of the research hotspots of CMfg, more and more studies are being undertaken on services selection and their combination especially the combination of heterogeneous services. However, the works related to homogeneous cloud services combinations are relatively few. After reviewing the existing works and noting certain limitations, a homogeneous cloud task distribution model was proposed, and an improved leapfrog algorithm for cloud task distribution (ILA-CTD) was designed to solve the model. The contributions of the paper are summarized as follows:
1) Compared to heterogeneous task distribution, there is relatively little research on homogeneous cloud tasks. A strategy of dealing with homogeneous tasks in the cloud environment was presented to bridge this gap.
2) A specific model was proposed to describe homogeneous cloud task distribution more precisely compared with alternative methods. An improved leapfrog algorithm was designed, which was proven to be more suitable for solving the proposed model.
3) The distribution of real manufacturing tasks of medical labeling machine bottom plates was presented as a case. It was shown that the proposed method provided a combination of factories with a high degree of quality similarity and high informationization under the constraints of factory capacity, task duration, and cost.
To promote the implementation of CMfg platforms with higher agility, future works should focus on the development of efficient demand-service matching algorithm. Personalized service customization should also be studied, because personalized demands from consumers are increasing.
Funding Statement: The research was financially supported by the National Science and Technology Major Project of China (No. 2019ZX04007001), the Science and Technology Major Project of Sichuan Province (No. 2020ZDZX0022).
Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.
1. Zhang, Y., Liu, J., Peng, Y., Dong, Y., Zhao, C. (2020). Performance analysis of intelligent CR-NOMA model for industrial IoT communications. Computer Modeling in Engineering & Sciences, 125(1), 239–257. DOI 10.32604/cmes.2020.010778. [Google Scholar] [CrossRef]
2. Xu, S., Chen, J., Wu, M., Zhao, C. (2021). E-commerce supply chain process optimization based on whole-process sharing of internet of things identification technology. Computer Modeling in Engineering & Sciences, 126(2), 843–854. DOI 10.32604/cmes.2021.014265. [Google Scholar] [CrossRef]
3. Giret, A., Garcia, E., Botti, V. (2016). An engineering framework for service-oriented intelligent manufacturing systems. Computers in Industry, 81, 116–127. DOI 10.1016/j.compind.2016.02.002. [Google Scholar] [CrossRef]
4. Nirmal Kumar, S. J., Ravimaran, S., Alam, M. M. (2020). An effective non-commutative encryption approach with optimized genetic algorithm for ensuring data protection in cloud computing. Computer Modeling in Engineering & Sciences, 125(2), 671–697. DOI 10.32604/cmes.2020.09361. [Google Scholar] [CrossRef]
5. Gong, Y., Guo, G. (2019). A data-intensive FLAC3D computation model: Application of geospatial big data to predict mining induced subsidence. Computer Modeling in Engineering & Sciences, 119(2), 395–408. DOI 10.32604/cmes.2019.03686. [Google Scholar] [CrossRef]
6. Li, B. H., Zhang, L., Wang, S. L., Tao, F., Cao, J. W. et al. (2010). Cloud manufacturing: A new service oriented networked manufacturing model. Computer Integrated Manufacturing Systems, 16, 1–7. DOI 10.13196/j.cims.2010.01.3.libh.004. [Google Scholar] [CrossRef]
7. Li, B. H., Zhang, L., Ren, L., Chai, X. D., Tao, F. et al. (2011). Further discussion on cloud manufacturing. Computer Integrated Manufacturing Systems, 17, 451–457. DOI 10.13196/j.cims.2011.03.3.libh.004. [Google Scholar] [CrossRef]
8. Argoneto, P., Renna, P. (2016). Supporting capacity sharing in the cloud manufacturing environment based on game theory and fuzzy logic. Enterprise Information Systems, 10(2), 193–210. DOI 10.1080/17517575.2014.928950. [Google Scholar] [CrossRef]
9. Correa, J. E., Toro, R., Ferreira, P. M. (2018). A new paradigm for organizing networks of computer numerical control manufacturing resources in cloud manufacturing. Procedia Manufacturing, 26(2), 1318–1329. DOI 10.1016/j.promfg.2018.07.132. [Google Scholar] [CrossRef]
10. Ren, L., Zhang, L., Wang, L., Tao, F., Chai, X. (2017). Cloud manufacturing: Key characteristics and applications. International Journal of Computer Integrated Manufacturing, 6(6), 501–515. DOI 10.1080/0951192X.2014.902105. [Google Scholar] [CrossRef]
11. Wu, Y., Jia, G., Cheng, Y. (2019). Cloud manufacturing service composition and optimal selection with sustainability considerations: A multi-objective integer bi-level multi-follower programming approach. International Journal of Production Research, 58(19), 6024–6042. DOI 10.1080/00207543.2019.1665203. [Google Scholar] [CrossRef]
12. Maheswari, S., Karpagam, G. R. (2018). Performance evaluation of semantic based service selection methods. Computers & Electrical Engineering, 71(5), 966–977. DOI 10.1016/j.compeleceng.2017.10.006. [Google Scholar] [CrossRef]
13. Eisa, M., Younas, M., Basu, K., Awan, I. (2020). Modelling and simulation of QoS-aware service selection in cloud computing. Simulation Modelling Practice and Theory, 103, 102108. DOI 10.1016/j.simpat.2020.102108. [Google Scholar] [CrossRef]
14. Chen, Z., Ming, X. (2020). A rough-fuzzy approach integrating best-worst method and data envelopment analysis to multi-criteria selection of smart product service module. Applied Soft Computing, 94, 106479. DOI 10.1016/j.asoc.2020.106479. [Google Scholar] [CrossRef]
15. Li, F., Liao, T. W., Zhang, L. (2019). Two-level multi-task scheduling in a cloud manufacturing environment. Robotics and Computer-Integrated Manufacturing, 56, 127–139. DOI 10.1016/j.rcim.2018.09.002. [Google Scholar] [CrossRef]
16. Chen, Y., Niu, Y. F., Li, J., Zuo, L. D., Wang, L. (2019). Task distribution optimization for multi-supplier collaborative production in cloud manufacturing. Computer Integrated Manufacturing Systems, 25, 1806–1816. DOI 10.13196/j.cims.2019.07.021. [Google Scholar] [CrossRef]
17. Liu, J., Chen, Y. (2019). A personalized clustering-based and reliable trust-aware QoS prediction approach for cloud service recommendation in cloud manufacturing. Knowledge-Based Systems, 174(1–4), 43–56. DOI 10.1016/j.knosys.2019.02.032. [Google Scholar] [CrossRef]
18. Eisa, M., Younas, M., Basu, K., Awan, I. (2020). Modelling and simulation of QoS—Aware service selection in cloud computing. Simulation Modelling Practice and Theory, 103, 102–108. DOI 10.1016/j.simpat.2020.102108. [Google Scholar] [CrossRef]
19. Zhao, L., Tan, W., Xie, N., Huang, L. (2020). An optimal service selection approach for service-oriented business collaboration using crowd-based cooperative computing. Applied Soft Computing, 92, 106270. DOI 10.1016/j.asoc.2020.106270. [Google Scholar] [CrossRef]
20. Hussain, A., Chun, J., Khan, M. (2020). A novel customer-centric methodology for optimal service selection (MOSS) in a cloud environment. Future Generation Computer Systems, 105, 562–580. DOI 10.1016/j.future.2019.12.024. [Google Scholar] [CrossRef]
21. Bouzary, H., Chen, F. F. (2020). A classification-based approach for integrated service matching and composition in cloud manufacturing. Robotics and Computer-Integrated Manufacturing, 66, 106989. DOI 10.1016/j.rcim.2020.101989. [Google Scholar] [CrossRef]
22. Poordavoodi, A., Goudarzi, M. R. M., Javadi, H. H. S., Rahmani, A. M., Izadikhah, M. (2020). Toward a more accurate web service selection using modifiedinterval DEA models with undesirable outputs. Computer Modeling in Engineering & Sciences, 123(2), 525–570. DOI 10.32604/cmes.2020.08854. [Google Scholar] [CrossRef]
23. Devi, R., Shanmugalakshmi, R. (2020). Cloud providers ranking and selection using quantitative and qualitative approach. Computer Communications, 154, 370–379. DOI 10.1016/j.comcom.2020.02.028. [Google Scholar] [CrossRef]
24. Gad-Elrab, A. A., Noaman, A. Y. (2020). A two-tier bipartite graph task allocation approach based on fuzzy clustering in cloud-fog environment. Future Generation Computer Systems, 103(11), 79–90. DOI 10.1016/j.future.2019.10.003. [Google Scholar] [CrossRef]
25. Gigliotta, O. (2018). Equal but different: Task allocation in homogeneous communicating robots. Neurocomputing, 272(3), 3–9. DOI 10.1016/j.neucom.2017.05.093. [Google Scholar] [CrossRef]
26. Sharma, V., Bala, M. (2020). An improved task allocation strategy in cloud using modified k-means clustering technique. Egyptian Informatics Journal, 21(4), 201–208. DOI 10.1016/j.eij.2020.02.001. [Google Scholar] [CrossRef]
27. Moussa, M., ElMaraghy, H. (2020). A genetic algorithm-based model for product platform design for hybrid manufacturing. Procedia CIRP, 93, 389–394. DOI 10.1016/j.procir.2020.04.044. [Google Scholar] [CrossRef]
28. Jiang, H., Yi, J., Chen, S., Zhu, X. (2016). A multi-objective algorithm for task scheduling and resource allocation in cloud-based disassembly. Journal of Manufacturing Systems, 41(4), 239–255. DOI 10.1016/j.jmsy.2016.09.008. [Google Scholar] [CrossRef]
29. Jatoth, C., Gangadharan, G. R., Fiore, U. (2019). Optimal fitness aware cloud service composition using modified invasive weed optimization. Swarm and Evolutionary Computations, 44(4), 1073–1091. DOI 10.1016/j.swevo.2018.11.001. [Google Scholar] [CrossRef]
30. Zhou, J., Gao, L., Yao, X., Zhang, C., Chan, F. T. et al. (2019). Evolutionary algorithms for many-objective cloud service composition: Performance assessments and comparisons. Swarm and Evolutionary Computation, 51, 100605. DOI 10.1016/j.swevo.2019.100605. [Google Scholar] [CrossRef]
31. Somasundaram, T. S., Govindarajan, K. (2014). CLOUDRB: A framework for scheduling and managing high-performance computing (HPC) applications in science cloud. Future Generation Computer Systems, 34(3), 47–65. DOI 10.1016/j.future.2013.12.024. [Google Scholar] [CrossRef]
32. Guo, Y., Tian, X., Fang, G., Xu, Y. (2020). Many-objective optimization with improved shuffled frog leaping algorithm for inter-basin water transfers. Advances in Water Resources, 138, 103531. DOI 10.1016/j.advwatres.2020.103531. [Google Scholar] [CrossRef]
33. Shampine, L. F. (2009). Stability of the leapfrog/midpoint method. Applied Mathematics and Computation, 208, 293–298. DOI 10.1016/j.amc.2008.11.029. [Google Scholar] [CrossRef]
34. Manimegalai-Sridhar, U., Govindarajan, A., Rhinehart, R. R. (2014). Improved initialization of players in leapfrogging optimization. Computers & Chemical Engineering, 60(2), 426–429. DOI 10.1016/j.compchemeng.2013.08.009. [Google Scholar] [CrossRef]
 | This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. |