

 | Computer Modeling in Engineering & Sciences |  |
DOI: 10.32604/cmes.2021.016403
ARTICLE
DEM Simulations of Resistance of Particle to Intruders during Quasistatic Penetrations
State Key Laboratory of Structural Analysis for Industrial Equipment, Dalian University of Technology, Dalian, 116023, China
*Corresponding Author: Shunying Ji. Email: jisy@dlut.edu.cn
Received: 03 March 2021; Accepted: 07 April 2021
Abstract: Based on the discrete element method and hydrostatics theory, an improved Archimedes principle is proposed to study the rules pertaining to resistance changes during the penetration process of an intruder into the particulate materials. The results illustrate the fact that the lateral contribution to the resistance is very small, while the tangential force of the lateral resistance originates from friction effects. Conversely, the resistance of particulate materials on the intruder mainly occurs at the bottom part of the intruding object. Correspondingly, the factors that determine the resistance of the bottom part of the intruding object and the rules pertaining to resistance changes are analyzed. It is found that when the volume density and friction coefficient of the particles and the radius of the bottom surface of the cylindrical intruder are varied, the resistance–depth curve consists of a nonlinear segment and a linear region. The intersection of the two stages occurs at the same location
Keywords: Particulate materials; improved Archimedes principle; quasistatic resistance; discrete element method
Granular media exist in natural environments and are extensively used in industrial productions. These types of media include natural particles like grain, and artificial particles like glass beads [1]. Despite extensive studies conducted during the last decade [2–4], neither the statics nor the dynamics of particulate materials are sufficiently understood [5]. One of the typical problems is the quasistatic penetration problem that plays a significant role in the static properties of particulate materials [6] and in the perturbation responses, such as the formation of shear bands [7,8], settlement effects [9], and the jamming transition [10–12]. Hence, this study aims to achieve an in-depth understanding of the resistance of particulate materials to intruders during the impact process, and to build a bridge between the static resistance and dynamic fluidity of particles.
To study the resistance of particulate materials to intruders, that reflects the complex physical properties of particulate materials in the process at which intruders impact dry particulate beds [13,14], it is necessary to build an interaction model involving the intruder and the particulate materials. In current research efforts, limited attention is being paid to quasistatic penetration processes [5,15]. Penetration dynamics depends on the intruder’s velocity and the microphysical characteristics of the impact system, such as the particle type, initial filling fraction, and the existence of interstitial fluid. Therefore, scholars a) considered the static or quasistatic effects, based on which the initial intruder velocity was found to be much lower than the sound velocity, and b) described the “slow” dynamics based on the macro force law when the intruder impacted the dry particles [16,17]. Scholars have established an empirical law to describe this process [18,19]: the resistance of the particulate materials with respect to the intruding object is mainly composed of the static resistance
In addition, the quasistatic resistance reflects the macroscopic properties of particulate materials, and there is a close relationship between the macroscopic performance of this type of media and the microscopic mechanism [25]. However, uncertainties lead to various difficulties in the study of the microscopic mechanisms. The phenomenological stages of the research focuses on the characterization of the law of motion of particulate materials [26]. The quasistatic problems are studied based on experiments, such as the distribution of the force chain measured based on photoelastic experiments [5,27] or the tracking of particle positions by a high-frequency camera to obtain the dynamic response of particles [13]. However, owing to the limitations of the current test and measurement methods, the accuracy of the results cannot be guaranteed [28]. Different numerical methods and models can be used in numerical simulations [29,30]. Specifically, the discrete element method (DEM) is the main tool used to simulate particulate materials {[31–33]}. The continuum-based model is suitable for simulating large asteroid impacts that can form large craters on planet surfaces. This study focuses on the influence of objects on particulate materials at the centimeter scale, where the continuum-based model is not applicable. DEM has been acknowledged to be one of the most effective numerical methods for simulations of particle dynamic behavior, and has been applied in a variety of research fields, such as in landslides, sandstorms, and in grain research [34–36]. Moreover, research studies have shown that the DEM is feasible for the study of particulate materials.
In this study, a numerical model is constructed to evaluate the penetration of an intruding object into particulate materials in the quasistatic state based on the use of the DEM. The variation of the resistance of the particulate materials with respect to the intruder is discussed based on the hydrostatics theory. The influence of the physical properties of particulate materials on the penetration process is recognized. Finally, the dependence of the resistance change on the intruder geometry is also discussed.
2 Discrete Element Method and Setup of Simulation Model
The spherical element and its nonlinear contact model are employed to calculate the interaction between particles to quantify the structural characteristics of particulate materials and their dynamic response during penetration. The contact forces of discrete elements can be divided into the normal contact force
where
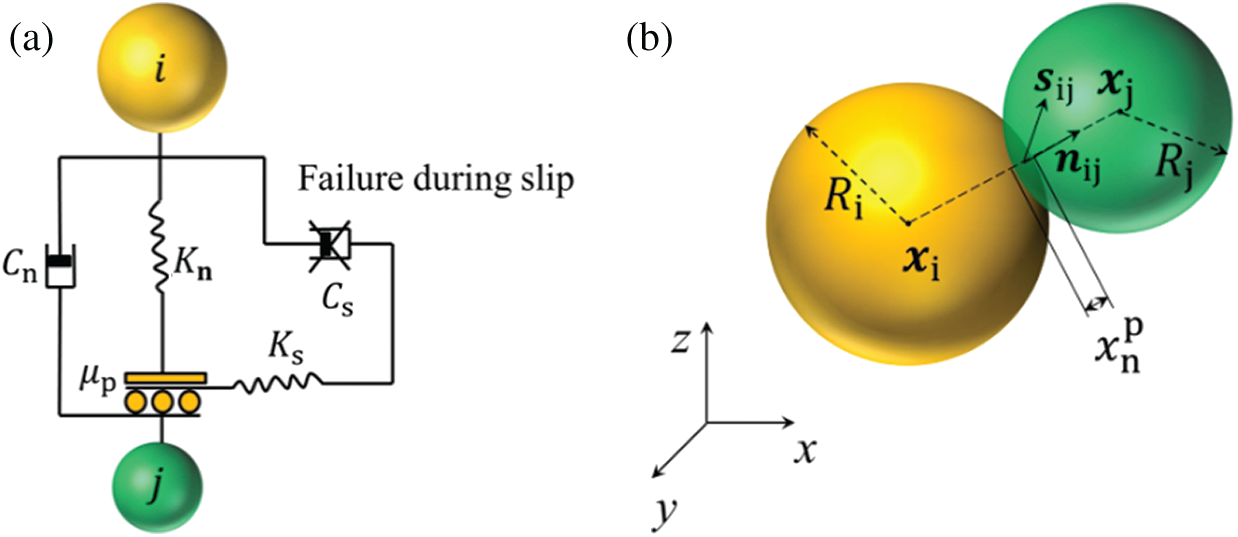
Figure 1: Contact model representation used in the discrete element model. (a) Contact model in normal and tangential directions (b) Contact model in the spherical discrete element
The contact force between particles is mainly composed of elastic and viscous force components, and the sliding friction—that is based on Coulomb’s friction—is also considered. The nonlinear Hertz–Mindlin contact model is used to calculate the elastic force between particles. In the normal direction, interparticle forces include the Hertzian elastic force and the nonlinear viscous force [37,38], expressed as,
where
where
In the nonlinear simplified Hertz–Mindlin (no-slip) contact model, the time step is not larger than the maximum time of contact of two particles. The time step is defined as,
where
where
The numerical simulation is performed using an in-house C++ code based on the theory described previous. A numerical simulation model is set up, as shown in Fig. 2. The cylindrical intruder penetrates the particulate materials at a low but constant velocity. That is to say, velocity-controlled loading is adopted for the intruder. To obtain effective results, the end point of the study is defined as the instant at which the entire cylinder penetrates into the particulate materials. The particles are dense packing in the container with a width
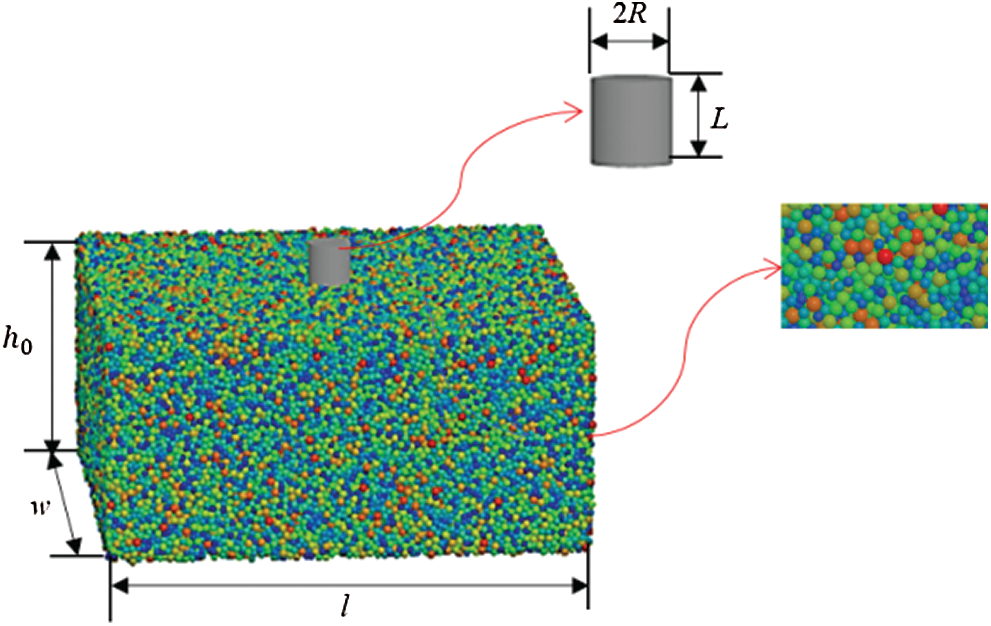
Figure 2: Schematic showing the penetration process of the cylindrical intruding object into the particulate materials based on which the numerical simulations were conducted
In the course of the penetration, the existence of the container boundary may generate a strong impact resistance, especially when the cylindrical intruder moves in a direction parallel to the container wall. The boundary effect is mainly caused by the interference inside the stress field of the particulate materials and the side wall [44,45]. To avoid this effect, the size of the container is large enough, and the cylindrical intruder penetration is set to occur in the middle of the container to eliminate the boundary effect [46]. Various particles are simulated by changing the relevant parameters of the particulate materials. The main simulation parameters are listed in Tab. 1.
3 Analysis of Quasistatic Resistance of Particulate Materials
To ensure that the entire research process is quasistatic, the velocity was chosen to take values in the range of 0.001–0.5 m/s to allow the penetration of the intruder into the particulate materials. Accordingly, the change of
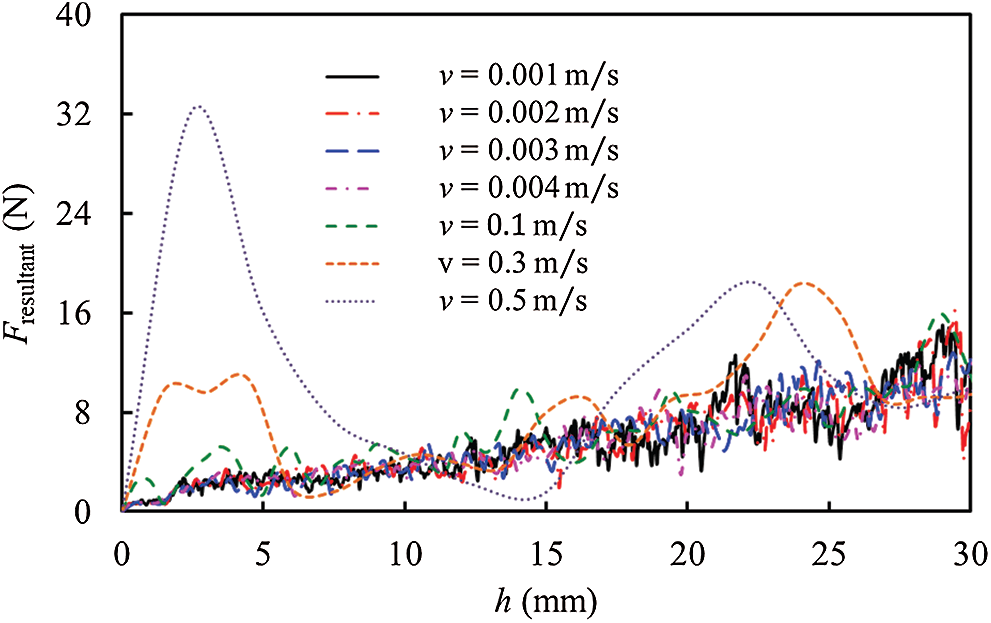
Figure 3: Resistance force data associated with the cylindrical intruder at different velocities
During the process of penetration, the particulate materials are mainly in contact with the bottom surface and the sides of the cylindrical intruding object, as shown in Fig. 4. Thus, interactions also occur on the bottom surface and on the sides. Fig. 5 shows the variations of the force
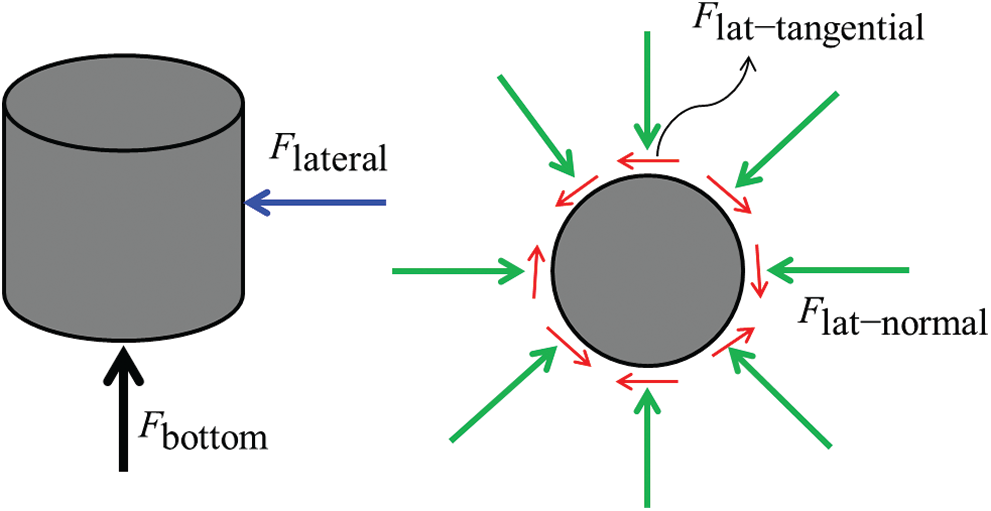
Figure 4: Schematic diagram of impact force on the intruding object
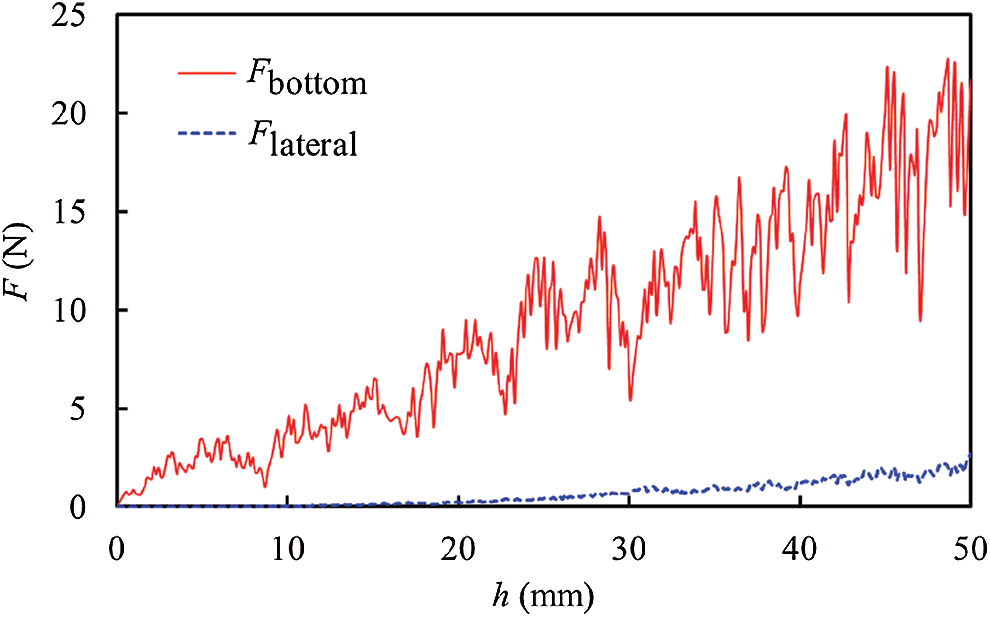
Figure 5: Resistance on different surfaces of the intruder as a function of the penetration depth
Even though the lateral force of the intruder is small, it does have an impact on the penetration process. The lateral force can be decomposed into the normal (
In this relation,
The values of the coefficients in Eq. (7) obtained by numerical simulations are
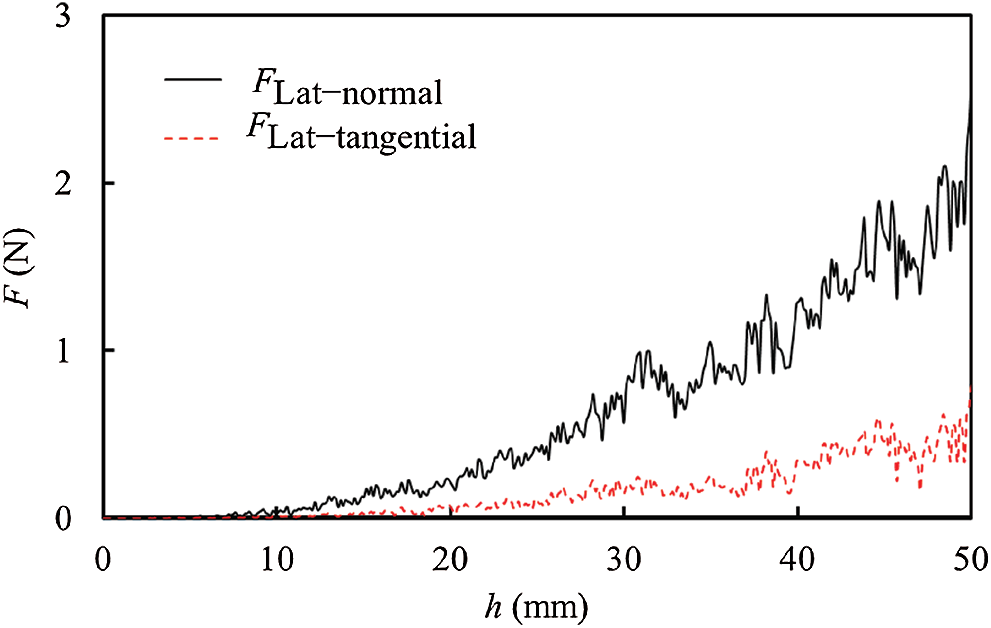
Figure 6: Relationships between lateral resistance and penetration depth for the normal and tangential force components
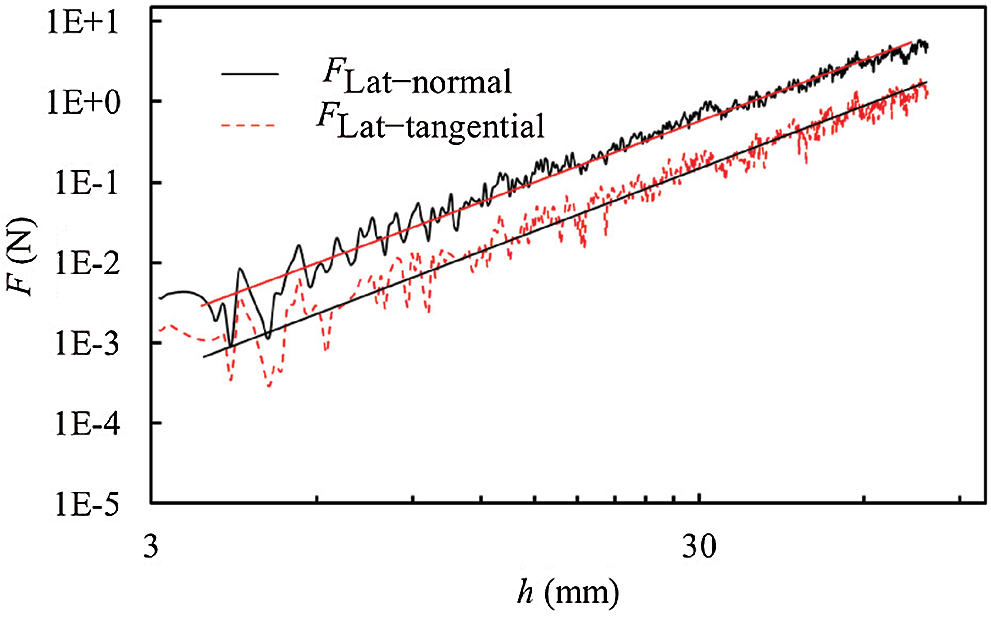
Figure 7: Lateral resistance as a function of the penetration depth
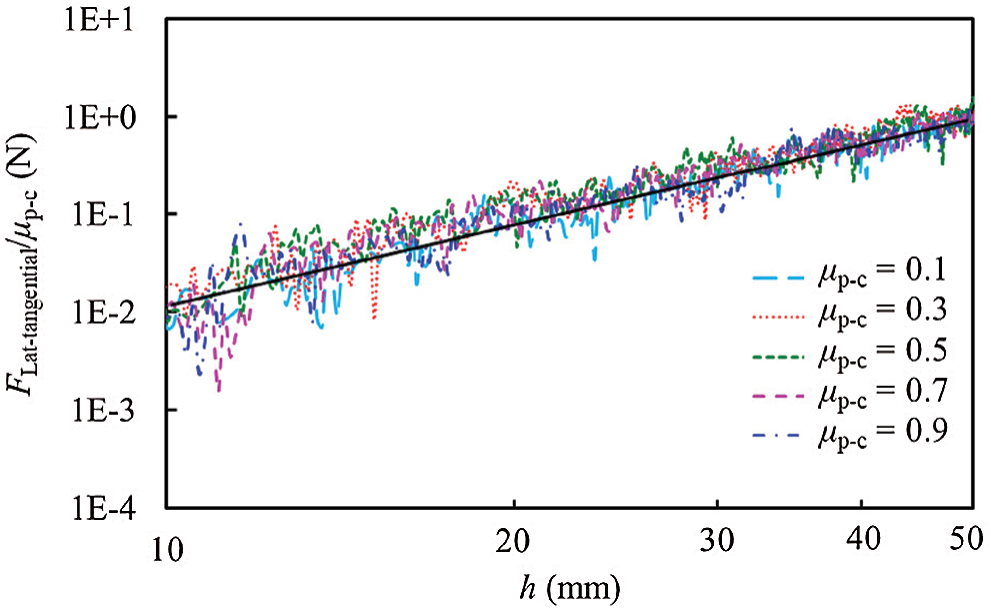
Figure 8: Effects of friction coefficients between intruder and particle on the tangential resistances
3.2 Determinants and Shape Dependence of the Force on the Bottom Surface of the Intruder
The bottom surface contributes a lot to the resistance of the cylindrical intruder, as shown in Fig. 5. The resistance–depth curve consists of the initial unstable segment and the linear segment. However, the initial unstable segment is not apparent, so the logarithm of the coordinate is used to obtain a better result. Fig. 9 shows the logarithmic change of the base resistance as a function of depth. The intersection of the two segments is defined as h0. The slope of the linear stage is K. To understand and explain the interaction between particulate materials and cylindrical intruders in the penetration process more clearly, it is necessary to clarify the true meaning of these two intervals and to determine the values of h0 and K.
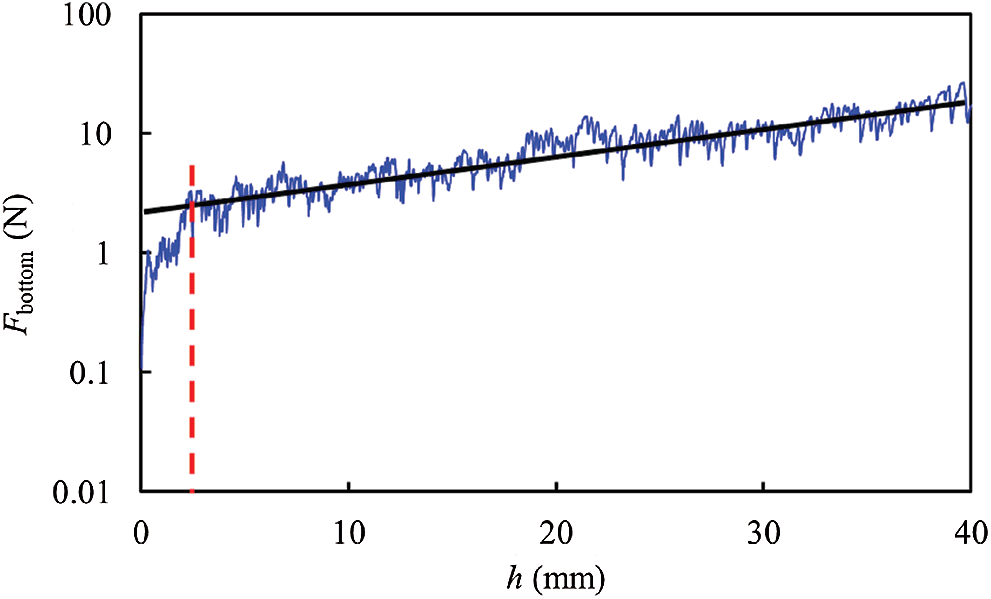
Figure 9: Resistance on the bottom surface (
The research conducted herein was based on a quasistatic state. Under quasistatic conditions, nonviscous, dry particulate materials can be regarded as a continuum, with a volume density
The results are shown in Figs. 10–11. When the coordinate is either the logarithm of the ratio of resistance to the area of the bottom surface (S), particle density (
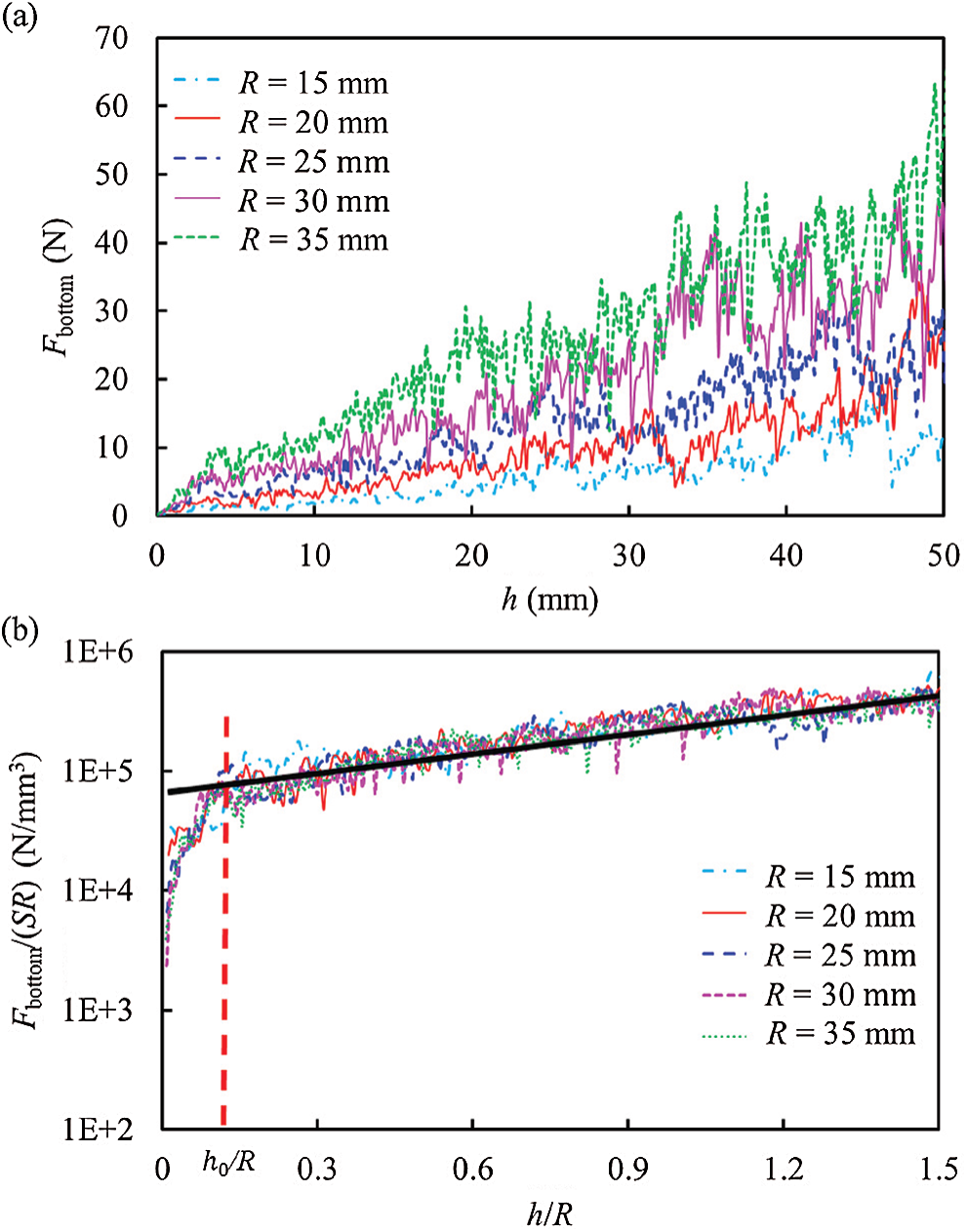
Figure 10: Changes in resistance on the bottom surface as a function of the penetration depth for different radii of cylindrical intruders. (a) Fbottom as a function of h (b) Fbottom/(SR) as a function of h/R

Figure 11: Plots showing the influences of particle densities. (a) Fbottom as a function of h. (b) Fbottom/ρ as a function of h/R
Therefore, we propose an improved Archimedes principle, whose normalization formula can be written as,
All simulations have yielded the relationship
There is speculation that in the initial stage of the penetration process, the particulate materials under the penetration cylinder formed an additional mass, and subsequently moved with the cylinder. This speculation has been confirmed [5]. The publication reports on findings in quasistatic conditions, and wedge blocks are generated under the circular foundation in which the taper angle of the wedge is
where
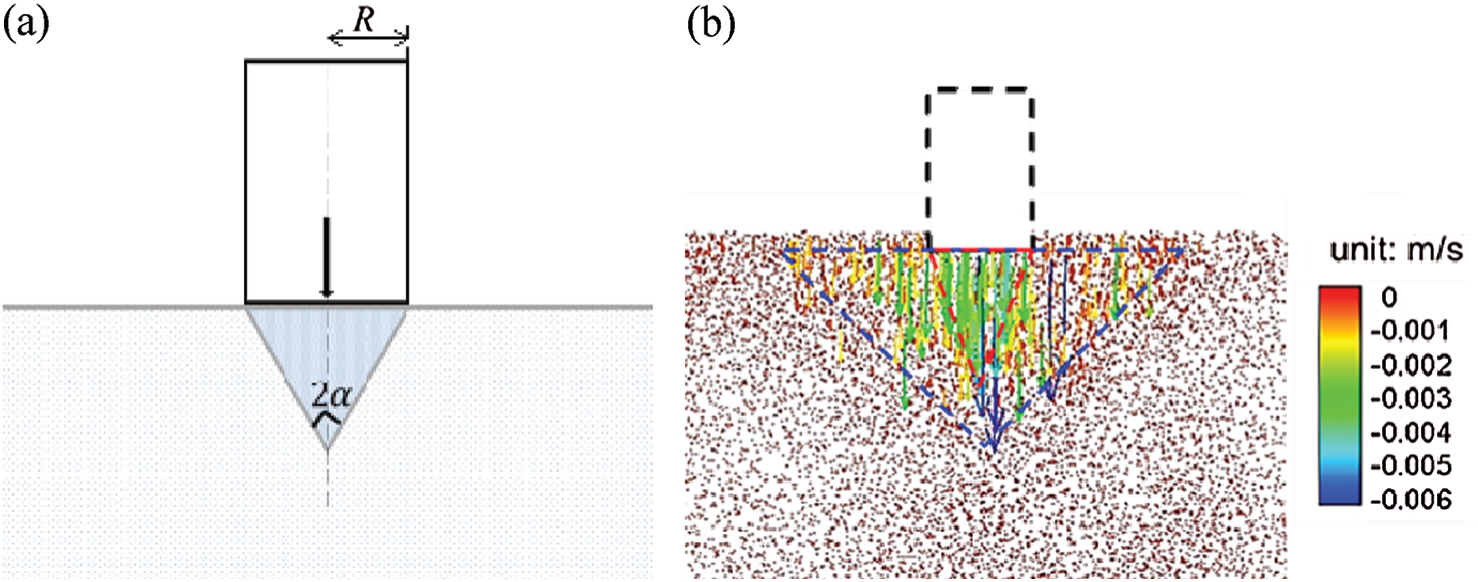
Figure 12: Wedge block generated under the circular foundation. (a) Schematic diagram of wedge block (b) Wedge blocks in the simulation result
After the rigid cone is formed, it moves forward in unison with the cylindrical intruder at the same speed. It separates particulate materials and the cylindrical intruder, that is, the resistance on the cylindrical intruder is caused by the contact friction between the particles on the surface of the rigid cone and other particles. It can be concluded that the slope of the linear stage should be related to the friction coefficient between the particulate materials. The slope of the linear stage is defined as
The relationship between the slopes and the friction coefficient is shown in Fig. 14. Accordingly, we can obtain the following relationship as,
This result is significance. It shows that the slope of the linear section is only related to the physical properties of particulate materials. To verify the correctness of the above results,
To determine whether
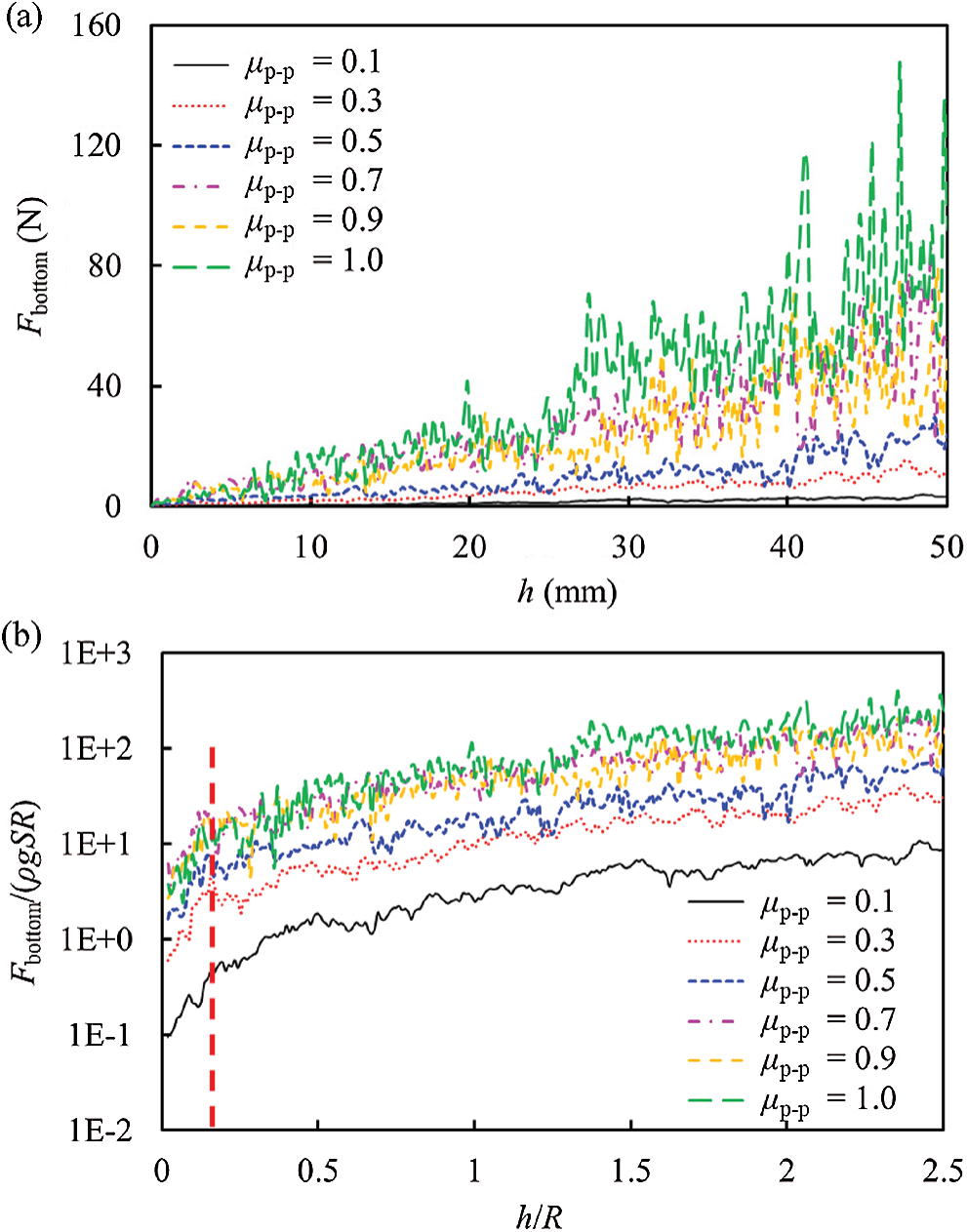
Figure 13: Dimensionless force–depth curves at different friction coefficients. (a) Fbottom as a function of h (b) Fbottom/(ρgSR) as a function of h/R
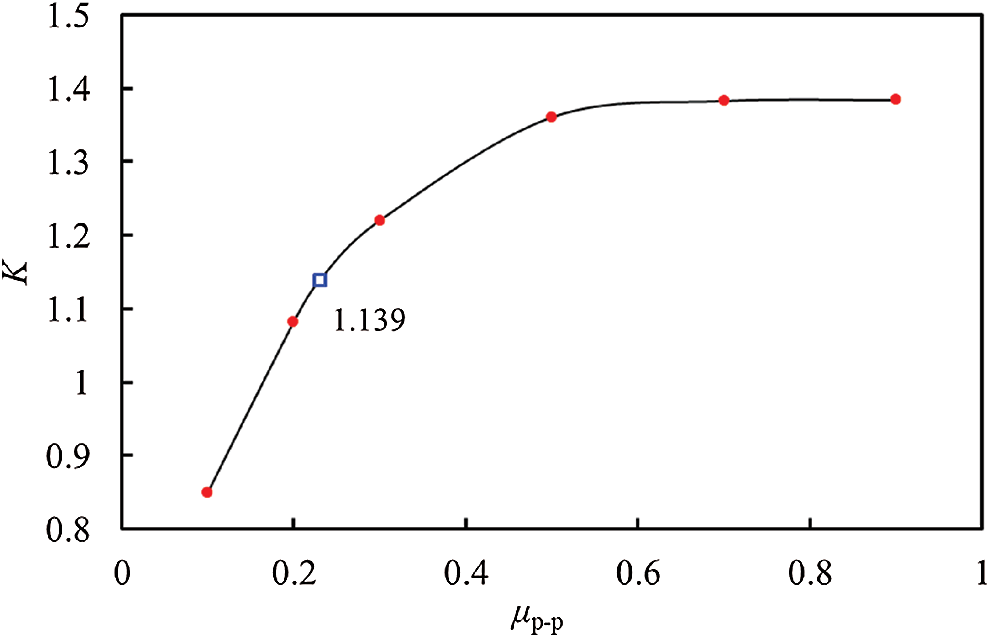
Figure 14: Slope variation at the linear stage obtained by numerical calculations as a function of the friction coefficient between the particles
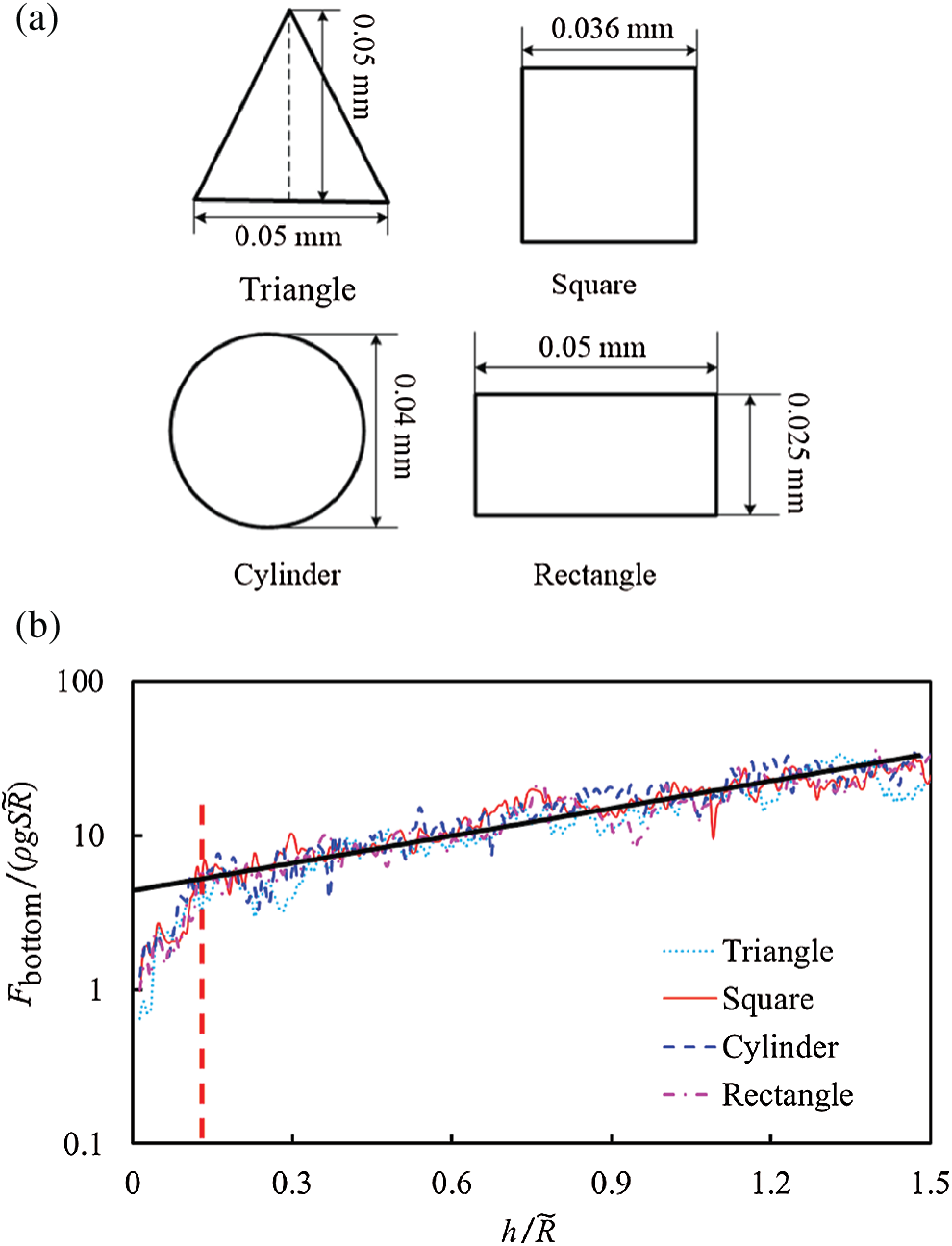
Figure 15: Force–depth curve is independent of the intruder’s cross-sectional shape (a) Cross-sectional shapes of different intruding objects (b) Resistances of the bottom surfaces of the intruder as a function of the penetration depth
In this study, the penetration resistance of particulate materials following the intrusion of a penetrating object was studied based on DEM simulations and the theory of hydrostatics in quasistatic conditions. During the penetration process, the intruder’s resistance was primarily associated with interactions on its bottom surface. The lateral contribution to the resistance was small. The tangential force of the lateral resistance was the friction effect of the normal component. These results were consistent with the experimental research premise that the influence of the friction between the intruder and the particulate materials could be neglected.
The determinants and the rules pertaining to the changes of resistance on the intruder’s bottom surface were analyzed according to the heterogeneity of particulate materials and based on an improved Archimedes principle. It was found that when the volume density and the friction coefficient of the particles were changed, and the radius of the bottom surface of the cylindrical intruder was altered, the resistance on the cylindrical intruder as a function of the penetration depth was divided into two sections.
Meanwhile, there were two resistance intervals associated with penetration depth changes, and the intersection of the two intervals occurred at
Funding Statement: This study was financially supported by the National Key Research and Development Program of China (Grant No. 2018YFA0605902) and the National Natural Science Foundation of China (Grant Nos. 11572067 and 11772085).
Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.
1. Zhuo, C. F., Yao, W. J., Wu, X. S., Feng, F., Xu, P. (2016). Research on the muzzle blast flow with gas-particle mixtures based on eulerian–eulerian approach. Journal of Mechanics, 32(2), 185–195. DOI 10.1017/jmech.2015.44. [Google Scholar] [CrossRef]
2. Ambroso, M. A., Kamien, R. D., Durian, D. J. (2005). Dynamics of shallow impact cratering. Physical Review E, 72(4), 41305–41308. DOI 10.1103/PhysRevE.72.041305. [Google Scholar] [CrossRef]
3. Royer, J. R., Corwin, E. I., Eng, P. J., Jaeger, H. M. (2007). Gas-mediated impact dynamics in fine-grained granular materials. Physical Review Letters, 99(3), 38003–38006. DOI 10.1103/PhysRevLett.99.038003. [Google Scholar] [CrossRef]
4. Jeng, F. S., Wang, T. T., Li, H. H., Huang, T. H. (2011). Influences of microscopic factors on macroscopic strength and stiffness of inter-layered rocks—revealed by a bonded particle model. Journal of Mechanics, 24(4), 379–389. DOI 10.1017/S1727719100002501. [Google Scholar] [CrossRef]
5. Kang, W., Feng, Y., Liu, C., Blumenfeld, R. (2018). Archimedes’ law explains penetration of solids into granular media. Nature Communication, 9(1), 1101–1109. DOI 10.1038/s41467-018-03344-3. [Google Scholar] [CrossRef]
6. Sakamura, Y., Komaki, H. (2011). Numerical simulations of shock-induced load transfer processes in granular media using the discrete element method. Shock Waves, 22(1), 57–68. DOI 10.1007/s00193-011-0347-6. [Google Scholar] [CrossRef]
7. Han, E., Peters, I. R., Jaeger, H. M. (2016). High-speed ultrasound imaging in dense suspensions reveals impact-activated solidification due to dynamic shear jamming. Nature Communication, 7(12243), 12243–12250. DOI 10.1038/ncomms12243. [Google Scholar] [CrossRef]
8. Namazian, Z., Najafi, A. F., Mousavian, S. M. (2016). Numerical simulation of particle-gas flow through a fixed pipe, using one-way and two-way coupling methods. Journal of Mechanics, 33(2), 205–212. DOI 10.1017/jmech.2016.53. [Google Scholar] [CrossRef]
9. Huang, L., Ran, X., Blumenfeld, R. (2016). Vertical dynamics of a horizontally oscillating active object in a two-dimensional granular medium. Physical Review E, 94(6), 62906–62912. DOI 10.1103/PhysRevE.94.062906. [Google Scholar] [CrossRef]
10. Vinutha, H. A., Sastry, S. (2016). Disentangling the role of structure and friction in shear jamming. Nature Physics, 12(6), 578–584. DOI 10.1038/nphys3658. [Google Scholar] [CrossRef]
11. Bi, D., Zhang, J., Chakraborty, B., Behringer, R. P. (2011). Jamming by shear. Nature, 480(7377), 355–358. DOI 10.1038/nature10667. [Google Scholar] [CrossRef]
12. Peters, I. R., Majumdar, S., Jaeger, H. M. (2016). Direct observation of dynamic shear jamming in dense suspensions. Nature, 532(7598), 214–221. DOI 10.1038/nature17167. [Google Scholar] [CrossRef]
13. Bester, C. S., Behringer, R. P. (2017). Collisional model of energy dissipation in three-dimensional granular impact. Physical Review E, 95(3), 32906. DOI 10.1103/PhysRevE.95.032906. [Google Scholar] [CrossRef]
14. Lin, J. H., Chang, K. C. (2015). Particle dispersion simulation in turbulent flow due to particle–particle and particle-wall collisions. Journal of Mechanics, 32(2), 237–244. DOI 10.1017/jmech.2015.63. [Google Scholar] [CrossRef]
15. Brzinski, T. A., Mayor, P., Durian, D. J. (2013). Depth-dependent resistance of granular media to vertical penetration. Physical Review Letters, 111(16), 168002–168008. DOI 10.1103/PhysRevLett.111.168002. [Google Scholar] [CrossRef]
16. Katsuragi, H., Durian, D. J. (2007). Unified force law for granular impact cratering. Nature Physics, 3(6), 420–423. DOI 10.1038/nphys583. [Google Scholar] [CrossRef]
17. Li, Y., Ji, W. (2013). Acceleration of coupled granular flow and fluid flow simulations in pebble bed energy systems. Nuclear Engineering and Design, 258, 275–283. DOI 10.1016/j.nucengdes.2013.02.032. [Google Scholar] [CrossRef]
18. Askari, H., Kamrin, K. (2016). Intrusion rheology in grains and other flowable materials. Nature Materials, 15(12), 1274–1279. DOI 10.1038/nmat4727. [Google Scholar] [CrossRef]
19. Aguilar, J., Goldman, D. I. (2016). Robophysical study of jumping dynamics on granular media. Nature Physics, 15(12), 278–284. DOI 10.1038/nphys3568. [Google Scholar] [CrossRef]
20. Clark, A. H., Behringer, R. P. (2013). Granular impact model as an energy-depth relation. Europhysics Letters, 101(6), 64001–64007. DOI 10.1209/0295-5075/101/64001. [Google Scholar] [CrossRef]
21. Garry, J. R. C., Towneti, M. C., Ba, A. J., Zarnecki, J. C., Marcou, G. (1999). The effect of ambient pressure and impactor geometry on low speed penetration of unconsolidated materials. Advances in Space Research, 23(7), 1229–1234. DOI 10.1016/S0273-1177(99)00189-1. [Google Scholar] [CrossRef]
22. Luding, S. (2008). Cohesive, frictional powders: Contact models for tension. Granular Matter, 10(4), 235–246. DOI 10.1007/s10035-008-0099-x. [Google Scholar] [CrossRef]
23. Uehara, J. S., Ambroso, M. A., Ojha, R. P., Durian, D. J. (2003). Low-speed impact craters in loose granular media. Physical Review Letters, 90(19), 194301–194305. DOI 10.1103/PhysRevLett.90.194301. [Google Scholar] [CrossRef]
24. Li, C., Zhang, T., Goldman, D. I. (2013). A terradynamics of legged locomotion on granular media. Science, 339(6126), 1408–1440. DOI 10.1126/science.1229163. [Google Scholar] [CrossRef]
25. Ambroso, M. A., Santore, C. R., Abate, A. R., Durian, D. J. (2004). Penetration depth for shallow impact cratering. Physical Review E, 71(5), 51305–51311. DOI 10.1103/PhysRevE.71.051305. [Google Scholar] [CrossRef]
26. Ma, L., Huang, D., Chen, W., Jiao, T., Sun, M. et al. (2017). Oscillating collision of the granular chain on static wall. Physics Letters A, 381(5), 542–548. DOI 10.1016/j.physleta.2016.12.011. [Google Scholar] [CrossRef]
27. Peters, J. F., Muthuswamy, M., Wibowo, J., Tordesillas, A. (2005). Characterization of force chains in granular material. Physical Review E, 72(4), 41307. DOI 10.1103/PhysRevE.72.041307. [Google Scholar] [CrossRef]
28. Wang, D., Zheng, X. (2013). Experimental study of morphology scaling of a projectile obliquely impacting into loose granular media. Granular Matter, 15(6), 725–734. DOI 10.1007/s10035-013-0446-4. [Google Scholar] [CrossRef]
29. Goldman, D. I., Umbanhowar, P. (2008). Scaling and dynamics of sphere and disk impact into granular media. Physical Review E, 77(2), 21308–21311. DOI 10.1103/PhysRevE.77.021308. [Google Scholar] [CrossRef]
30. Gravish, N., Goldman, D. I. (2010). Force and flow transition in plowed garticle media. Physical Review Letters, 105(12), 128301–128304. DOI 10.1103/PhysRevLett.105.128301. [Google Scholar] [CrossRef]
31. Kuang, S. B., Lamarche, C. Q., Curtis, J. S., Yu, A. B. (2013). Discrete particle simulation of jet-induced cratering of a granular bed. Powder Technology, 239, 319–336. DOI 10.1016/j.powtec.2013.02.017. [Google Scholar] [CrossRef]
32. Wada, K., Senshu, H., Matsui, T. (2006). Numerical simulation of impact cratering on granular material. Icarus, 180(2), 528–545. DOI 10.1016/j.icarus.2005.10.002. [Google Scholar] [CrossRef]
33. Ciamarra, M. P., Lara, A. H., Lee, A. T., Goldman, D. I., Vishik, I. et al. (2004). Dynamics of drag and force distributions for projectile impact in a granular medium. Physical Review Letters, 92(19), 194301. DOI 10.1103/PhysRevLett.92.194301. [Google Scholar] [CrossRef]
34. Li, Y., Dove, A., Curtis, J. S., Colwell, J. E. (2016). 3D DEM simulations and experiments exploring low-velocity projectile impacts into a granular bed. Powder Technology, 288, 303–314. DOI 10.1016/j.powtec.2015.11.022. [Google Scholar] [CrossRef]
35. Cleary, P. W. (2001). Recent advances in DEM modelling of tumbling mills. Minerals Engineering, 14(10), 1295–1319. DOI 10.1016/S0892-6875(01)00145-5. [Google Scholar] [CrossRef]
36. Weng, M. C., Cheng, C. C., Chiou, J. S. (2013). Exploring the evolution of lateral earth pressure using the distinct element method. Journal of Mechanics, 30(1), 77–86. DOI 10.1017/jmech.2013.73. [Google Scholar] [CrossRef]
37. Wang, C., Deng, A., Taheri, A., Zhao, H. H., Li, J. (2019). Modelling particle kinetic behaviour considering asperity contact: Formulation and DEM simulations. Granular Matter, 21(2), 16–31. DOI 10.1007/s10035-019-0868-8. [Google Scholar] [CrossRef]
38. Su, Y., Cui, Y., Ng, C. W. W., Choi, C. E., Kwan, J. S. H. (2019). Effects of particle size and cushioning thickness on the performance of rock-filled gabions used in protection against boulder impact. Canadian Geotechnical Journal, 56(2), 198–207. DOI 10.1139/cgj-2017-0370. [Google Scholar] [CrossRef]
39. Bahaaddini, M., Sharrock, G., Hebblewhite, B. K. (2013). Numerical direct shear tests to model the shear behaviour of rock joints. Computers and Geotechnics, 51(4), 101–115. DOI 10.1016/j.compgeo.2013.02.003. [Google Scholar] [CrossRef]
40. Ji, S., Shen, H. H. (2006). Characteristics of temporalspatial parameters in quasisolid-fluid phase transition of granular materials. Chinese Science Bulletin, 51(6), 646–654. DOI 10.1007/s11434-006-0646-y. [Google Scholar] [CrossRef]
41. Han, K., Feng, Y. T., Owen, D. R. J. (2007). Performance comparisons of tree-based and cell-based contact detection algorithms. Engineering Computations, 24(2), 165–181. DOI 10.1108/02644400710729554. [Google Scholar] [CrossRef]
42. Di Renzo, A., Di Maio, F. P. (2004). Comparison of contact-force models for the simulation of collisions in DEM-based granular flow codes. Chemical Engineering Science, 59(3), 525–541. DOI 10.1016/j.ces.2003.09.037. [Google Scholar] [CrossRef]
43. Li, Y., Ji, S. (2018). A geometric algorithm based on the advancing front approach for sequential sphere packing. Granular Matter, 20(4), 58–69. DOI 10.1007/s10035-018-0833-y. [Google Scholar] [CrossRef]
44. Stone, M. B., Bernstein, D. P., Barry, R. (2004). Stress propagation getting to the bottom of a particle medium. Nature, 427(6972), 503–505. DOI 10.1038/427503a. [Google Scholar] [CrossRef]
45. Seguin, A., Bertho, Y., Gondret, P. (2008). Influence of confinement on granular penetration by impact. Physical Review E, 78(1), 10301–10304. DOI 10.1103/PhysRevE.78.010301. [Google Scholar] [CrossRef]
46. Nelson, E. L., Katsuragi, H., Mayor, P., Durian, D. J. (2008). Projectile interactions in granular impact cratering. Physical Review Letters, 101(6), 68001–68006. DOI 10.1103/PhysRevLett.101.068001. [Google Scholar] [CrossRef]
47. Viswanathan, K., Mahato, A., Murthy, T. G., Koziara, T., Chandrasekar, S. (2015). Kinematic flow patterns in slow deformation of a dense granular material. Granular Matter, 17(5), 553–565. DOI 10.1007/s10035-015-0576-y. [Google Scholar] [CrossRef]
48. Wu, X., Zhong, S., Ling, D., Chen, Y. (2012). Model test study of vertical impact of space lander footpad. Rock and Soil Mechanics, 33(4), 1045–1050. DOI 10.16285/j.rsm.2012.04.007. [Google Scholar] [CrossRef]
 | This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. |