Computer Modeling in Engineering & Sciences

DOI: 10.32604/cmes.2021.014530

ARTICLE

An Effective Feature Modeling Approach for 3D Structural Topology Design Optimization

Fusheng Qiu1,*, Hongliang Liu1,* and Hongjuan Zhao2

1College of Aerospace Engineering, Shenyang Aerospace University, Shenyang, 110136, China
2Chengdu Aircraft Industrial (Group) Co., Ltd., Chengdu, 610092, China
*Corresponding Authors: Fusheng Qiu. Email: qfsmaple@163.com; Hongliang Liu. Email: liuhongliang@sau.edu.cn
Received: 06 October 2020; Accepted: 10 December 2020

1  Introduction

Topology optimization is an advanced design approach which aims at finding appropriate material distribution within a prescribed domain. At present, there have been rapid development and extensive applications for topology optimization of continuum structures, which has been successfully applied to acoustics, electromagnetics, optics, etc. And numerous topology optimization methods have been proposed, such as the homogenization method [1], solid isotropic material with penalization (SIMP) method [2–4], evolutionary optimization (ESO/BESO) method [5,6], level set method [7–9], moving morphable component/void method (MMC/MMV) [10,11], and Feature-driven topology optimization method [12]. Notably, the density-based SIMP (solid isotropic material with penalization) method has been popularly adopted because of its conceptual simplicity and easy implementation, and it has been successfully implemented in commercial software systems, such as ANSYS, OptiStruct, Tosca. For an overview of topology optimization approaches and their applications, the readers are referred to the monograph [13] and the review articles [14–17].

Feature modeling technology is known as a new milestone for the development of CAD/CAM. It is an application technology with complex work but good development prospects [18,19]. The study of features is mainly related to identifying and extracting parts so as to get the geometric model of parts. Then, the process programming, technical coding and numerical control coding are carried out to realize the automatic control process. On the other hand, in the process of engineering application, some optimization results are difficult to be applied to practical projects due to complex constraints, special engineering requirements and technical conditions [20–24]. It should be noted that more and more attention has been paid to the research of structural topology optimization considering feature constraints because such optimization results are closer to the engineering practice, which shows a better application prospect [25,26].

The studies of feature-based topology optimization mainly focus on four aspects: (1) Introducing feature constraints (constraint model) into the constraint formulation of the optimization model, such as the CAO and SKO algorithm proposed by [20] and the manufacturing-oriented hierarchical optimization method [21]; (2) A domain-oriented constraint model is established for specific or typical applications, such as the introduction of feature constraint model into the density-based method in [22,23]; (3) Transforming constraint functions into design variables through models (i.e., transforming to unconstrained optimization problems), such as a unified projection-based approach for topology optimization with manufacturing constraints [27], and constraints transformed into design variables for master slave relationships with use of the connecting variables in [28]; (4) The constraints are simplified or modeled, such as the topology and thickness optimization of laminated composites including manufacturing constraints by Sørensen et al. [29]. Additionally, an optimization model with manufacturing process constraints was established in [30], and an identification method was developed for enclosed voids restriction in manufacturability design for additive manufacturing structures [31]. Recently, a feature-driven topology optimization method was proposed, which included fewer design variables, considering both components and structures as designable engineering features [12,32]. And the feature-driven method was then successfully applied in the bio-inspired rudder structure design and the multiscale topology design problems [33,34].

This paper aims to develop an effective and efficient feature modeling approach to achieve the optimal topology designs of 3D structure with feature constraints. Different from the traditional method which requires complicated constraint processing, the purpose of this method is to design a structure with predetermined features more directly and easily. To this end, the extensible constraint factors are introduced into the feature modeling, and the feature is linked with the constraint factors by feature matching technique. And it can be flexibly applied to the structure design with added holes by changing the constraint factors to increase holes with different shapes. Thus, the topological optimization method of continuum structures can be more suitable for engineering applications. Not only the features are introduced in the process of topology optimization, but also the feature model and optimization model are relatively independent. Theoretically, the feature modeling approach can be extended and introduced into various topology optimization methods and problems. In the present work, the widely used density method is employed, and the structural design problem is solved under the formulation of maximizing the stiffness of a structure considering the constraint of material volume.

The remainder of this paper is organized as follows. In Section 2, the feature modeling approach is presented for topology design optimization. In Section 3, the Feature-based 3D structural topology optimization model is given. The numerical solution aspects are presented in Section 4. In Section 5, the effectiveness of the proposed approach is demonstrated by several benchmark tests. Main conclusions are finally drawn in Section 6.

2  Feature Modeling Approach

2.1 Basic Idea

Features include the definition information of product, various information related to the design and manufacturing of product. In the topology optimization method, the introduction of feature makes the design intention more directly reflected, and makes the established product model easier to understand and organize for production. In order to solve the design problem of engineering application, it needs simplifying for each problem before implementation of the core algorithm for topology optimization in the traditional method. Then, the process of modeling and meshing is completed. However, the process of modeling is relatively complex, and unreasonable models still need to be changed. Such a large amount of complex pre-processing has the disadvantages of large workload, uncontrollable and non-standard, which leads to the inconvenience of application.

In order to solve the complex pre-processing problem in the traditional methods, a feature modeling technology is introduced in the present work, and different problems are simplified including extracting and combining the features to establish basic feature models, and then an adaptive feature model library is formed based on the loads. The proposed method selects the appropriate pseudo-density of elements for different feature models and introduces constraint factors to control various feature models. When dealing with practical engineering problems, different constraint factors are selected according to the design requirements to facilitate the retrieval in the feature model library, and the feature models that meet the structural requirements are found to implement the core algorithm of topology optimization, as shown in Fig. 1.

Figure 1: The procedure flowchart of the present feature-based optimization method

2.2 Constraint Factor

In the present feature modeling approach, the constraint factors are introduced to simplify the engineering design problem. The specific constraint expression is separated from the design variable (pseudo density), which is conducive to the extensibility of the topology optimization model. Namely, the constraint condition can be changed as needed in the practical application without changing the form of topology optimization model. By changing the values of the constraint factors, the topology optimization model and the constraint model are considered separately.

Specifically, the design variable with constraint factor is a vector. According to the actual design requirements, it can be defined as:

xenew=[xe,λ](1)

where the design variable xenew is a vector composed of xe and λ, and it ranges from 0 to 1. It should be noted that xe is the traditional pseudo density of element, and it ranges from xmin to 1, namely 0<xmin≤xe≤1. Therein, λ indicates the constraint factor, and it can be defined as the collaborative determination of various constraints. For example, the constraint factor λ can be defined as:

λ={ζ⇔xenew=ζxe0⇔xenew=xe-1⇔xenew=xmin(2)

where ζ denotes the weight coefficient associated with the constraint condition, and its range is 0<xmin/xe≤ζ≤1. When λ is equal to ζ, xenew is equal to ζxe, namely the elemental pseudo density is changed according to the constraint condition; When λ is equal to zero, xenew is equal to xe, namely the iteration is performed according to the traditional density method. When λ is equal to −1, xenew is equal to xmin, namely the value of elemental pseudo density remains unchanged. The introduction of constraint factor makes it unnecessary to establish the specific analytical expression of constraints and some penalty factors in topology optimization methods, thus it is convenient for the model expression of feature constraint utilizing the proposed feature modeling approach. At the same time, it is easy to realize batch processing of pseudo-density, thus the design efficiency of topology optimization can be improved.

2.3 Topology Optimization Formulation

In order to improve the engineering practicality, the constraint factor controlled by different design requirements is introduced into the pseudo-density function. Therefore, the pseudo density as well as the whole design optimization iteration is affected by the constraint factor. In the topology optimization model with feature constraint, the pseudo-density value of element xmin is used to replace the traditional element density xe in the variable density method. The corresponding formulation of topology optimization can mathematically be stated as:

Find:xnew={x1new,x2new,…xenew,…,xnnew}T∈Rn,xenew=[xe,λ],e=1,…,nMin:C=FTU=UTKU=∑e=1nueTkeue=∑e=1nf(xenew)ueTk0ue

Subjectto:V=f⋅V0=∑e=1nxenewve≤V¯,F=K⋅U,0<xmin≤xenew≤1(3)

where C denotes the mean compliance of a structure, F is the global load vector, and U means the global displacement vector. ue is the elemental displacement vector, ke is the elemental stiffness matrix with pseudo density and k0 is the elemental stiffness matrix of fully solid material. V is the volume function, and V¯ indicates the upper bound of the structural volume. V0 is the initial volume of a structure and f denotes the prescribed volume ratio. Furthermore, xnew is the design variable, xe is determined by

Eq(xe)=Emin+xe⋅(E0-Emin)/(1+q(1-xe))(4)

In Eq. (3), xmin is a small positive number for lower bound to avoid singularity in stiffness matrix. In the present work, it is set as xmin=0.001.

3  Feature-Based 3D Topology Optimization Model

3.1 Shape Feature

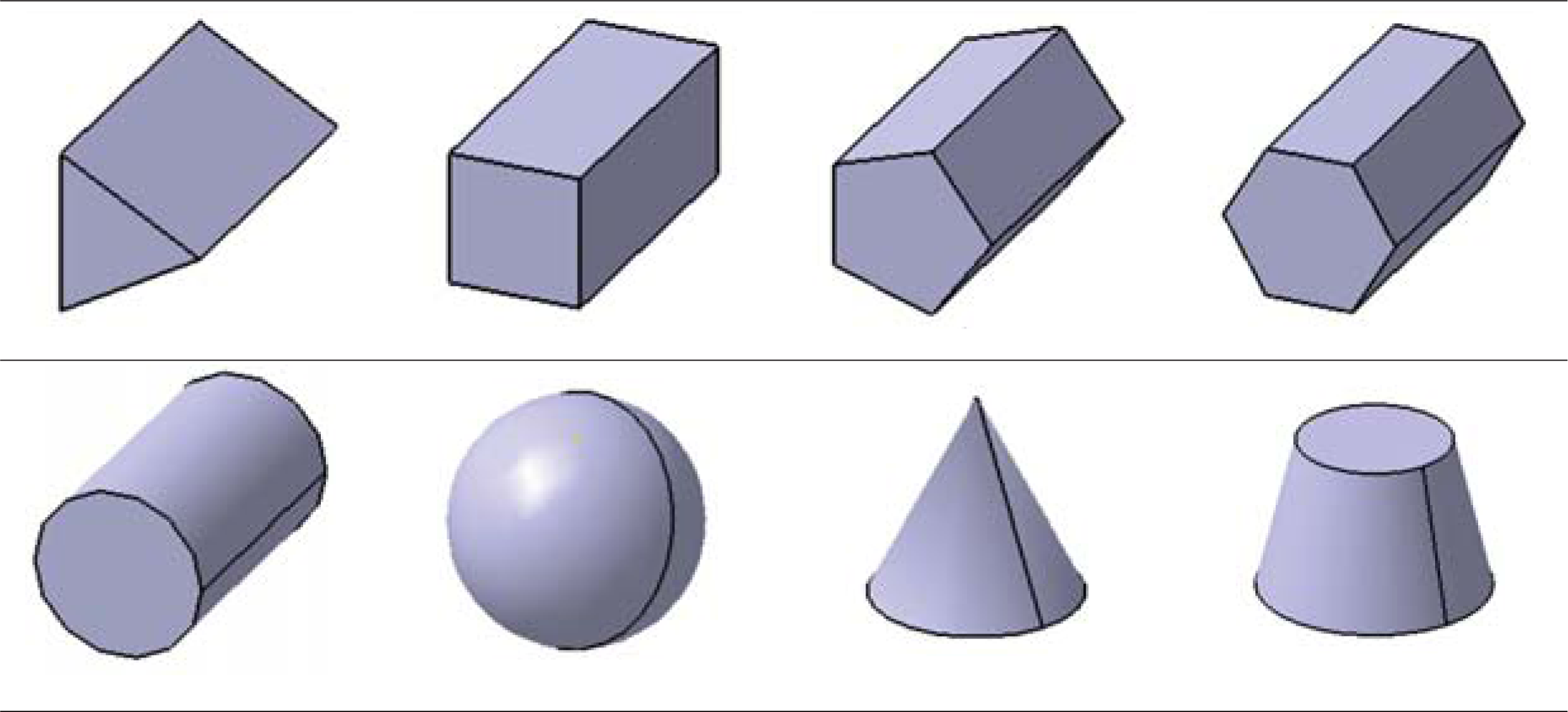
The shape features are particular shapes formed by a group of geometric elements with certain topological relation on the part. They have a specific function and a specific set of machining methods. The shape features can be divided into basic features and additional features. The basic features are used to construct the main shape of the parts (such as cylinder, cone, etc.), and the additional features are used to modify the local features (such as all kinds of holes, chamfering, etc.). Additional features are attached to the basic features. Any part is composed of a basic feature and several additional features.

3.1.1 Basic Feature

The basic feature is the basic geometry of the construction parts, mainly refers to the cylinder, cone, form, cuboid, sphere and other simple basic geometry solid. Solid models have perfect topological structure and geometric information, and are widely used in part modeling. It can automatically detect the boundary without cracks and incomplete information, which are the basis of part modeling and the primary task of the whole design process. Some of the basic feature models are listed in Tab. 1.

Table 1: Solid feature model

3.1.2 Additional Feature

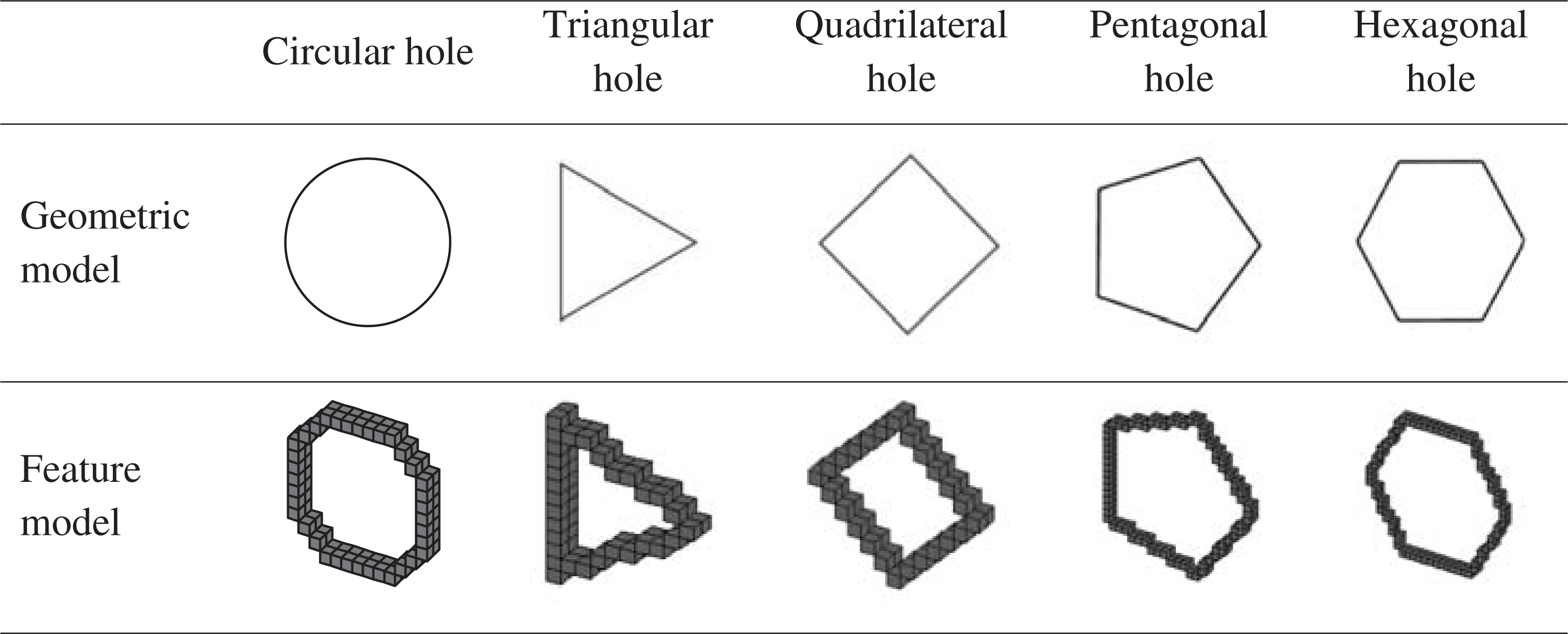
The additional features are geometric features attached to the basic feature, mainly referring to various types of hole, keyway, chamfering, etc., which are part modifications of the basic feature and reflect the subtle structure of the geometric shapes of the parts. The feature of hole is an important engineering feature, which is used in the modeling of many parts. It should be specified for the placement of hole, location dimension and size dimension when creating the feature of a hole. The characteristics of each type of hole are summarized in Tab. 2.

Table 2: Geometric model and feature model

3.1.3 Boolean Operation

Boolean operation is an operation that generates new features of two or more geometries in the entity model above by adding (as shown in Fig. 2), subtracting (as shown in Fig. 3), and intersecting (as shown in Fig. 4). Through the Boolean operation of CAD (computer aided design) software, it has a breakthrough effect in the geometry modeling. Flexible application can reduce the operation of geometry model, improve the quality of modeling, and simplify the modeling difficulty of complex geometry model, so as to make the feature modeling of geometry more reasonable.

Figure 2: Boolean union model

Figure 3: Boolean subtraction model

Figure 4: Boolean intersection model

3.2 Feature Description for 3D Topology Optimization

In the practical engineering, the feature models can be expressed with use of the feature modeling techniques based on various features, which are connected by feature models and topology optimization algorithms. In order to realize the description of the feature model, a (D; S; C) triples is introduced. Therein, D{d1,d2,…,di} is the design space and size of the feature; S{s0,s1,s2,…,sj} contains the identifier of feature (s0), the feature matching condition and evaluation criteria (s1,s2,…,sj); C{c1,c2,c3} is the value of the constraint function for the feature-based topology optimization, c1 is defined as the matching lower limit value, c2 is the matching upper limit value, and c3 is the feature configuration value. For example, the design feature of a round hole is shown in Fig. 5. The feature constraint value is 0.8, and it can be expressed as: d1 = d2 = 12, d3 = 2, d4=[0 0 1]; s0=Circle001, s1 = 0.5; c1=xmin, c2 = 1, c3 = 0.8, where xmin can be directly recorded as the minimum value of the elemental pseudo density.

Figure 5: Hole and its feature display

In order to make the feature model more suitable for the practical application of engineering, the feature description is expressed as the feature matrix oriented to the topology optimization algorithm. The feature constraint is transformed into a matrix expression which can be applied to the optimization algorithm. In the process of feature extraction, a discrete feature matrix Me with dimension determined by D can be formed according to the feature model. For example, the feature model in Fig. 5 can be described by a 13×13×2 numerical matrix. The coding rules of node elements (regular hexahedron) are from top to bottom, from left to right (clockwise), from front to back, and from small to large (as shown in Fig. 6). The position coordinates (i, j, k) and the unique identification ID of nodes in the matrix are calculated according to Eqs. (5) and (6). The feature model is calculated based on the element stiffness matrix as shown in Fig. 7.

ID=i×ne+(ne-j)+k×ne×me (5)

me=d1dx+1,ne=d2dy+1,pe=d3dz+1 (6)

where i∈[1,me], j∈[1,ne], k∈[1,pe], d1, d2 and d3 are the elements of constraint design space D, and dx, dy and dz are elemental dimensions.

Figure 6: Feature element coding

Figure 7: The solution of feature model

In order to make the feature matrix of the feature constraint match the whole design space, the element feature matrix [Me]me×ne×pe need to be extended to the global feature matrix consistent with the overall design space, according to the position of constraints in the overall design space P(x0, y0, z0) (namely the front lower left). Then, the value of xenew is calculated by Eq. (4), and xenew can be used for iteration calculation. Therefore, the feature constraints can be introduced into the algorithm of topology optimization.

P⇒(i0=x0dx,j0=y0dy,k0=z0dz)Me=[(aijk)|aijk={c1Ge∩Ω=φc2Ge=Ωc3Ge⊆Ω0ge∉Ω]me×ne×peMeS0=[(aijk)|a(i+i0)(j+j0)(k+k0)S0={aijk(i,j,k)∈(me,ne,pe)0(i,j,k)∈(me,ne,pe)]m×n×pxenew=[xe×(1+∑ λaijkS0)|e(ijk)∈(m,n,p),λ={ζaijkS0=c2,c30aijkS0=0-1aijkS0=c1](7)

where Ω denotes the set of feature boundary, and the sets of elemental matrix are represented by Ge{g1,g2,…,ge,…}. For Boolean operation, it can also be applied to the matrix expression of topology optimization algorithm. In order to match the feature matrix of Boolean operation with the overall design space, the Boolean operation model was introduced into the optimization algorithm by calculating xenew. For example in Fig. 3 triangular hole was made in the regular pentagonal prism through Boolean subtraction model.

4  Numerical Solution Aspects

The proposed feature modeling approach for 3D structural topology optimization opens up the relatively independent variable xenew for the introduction of feature into the core algorithm of topology optimization, and its application process is shown in Fig. 8. The corresponding topology optimization process is shown in Fig. 9. It should be noted that the elemental form in the discrete process of Step 2 must be consistent with the topology optimization model. Otherwise, the transformation is carried out in Step 3.

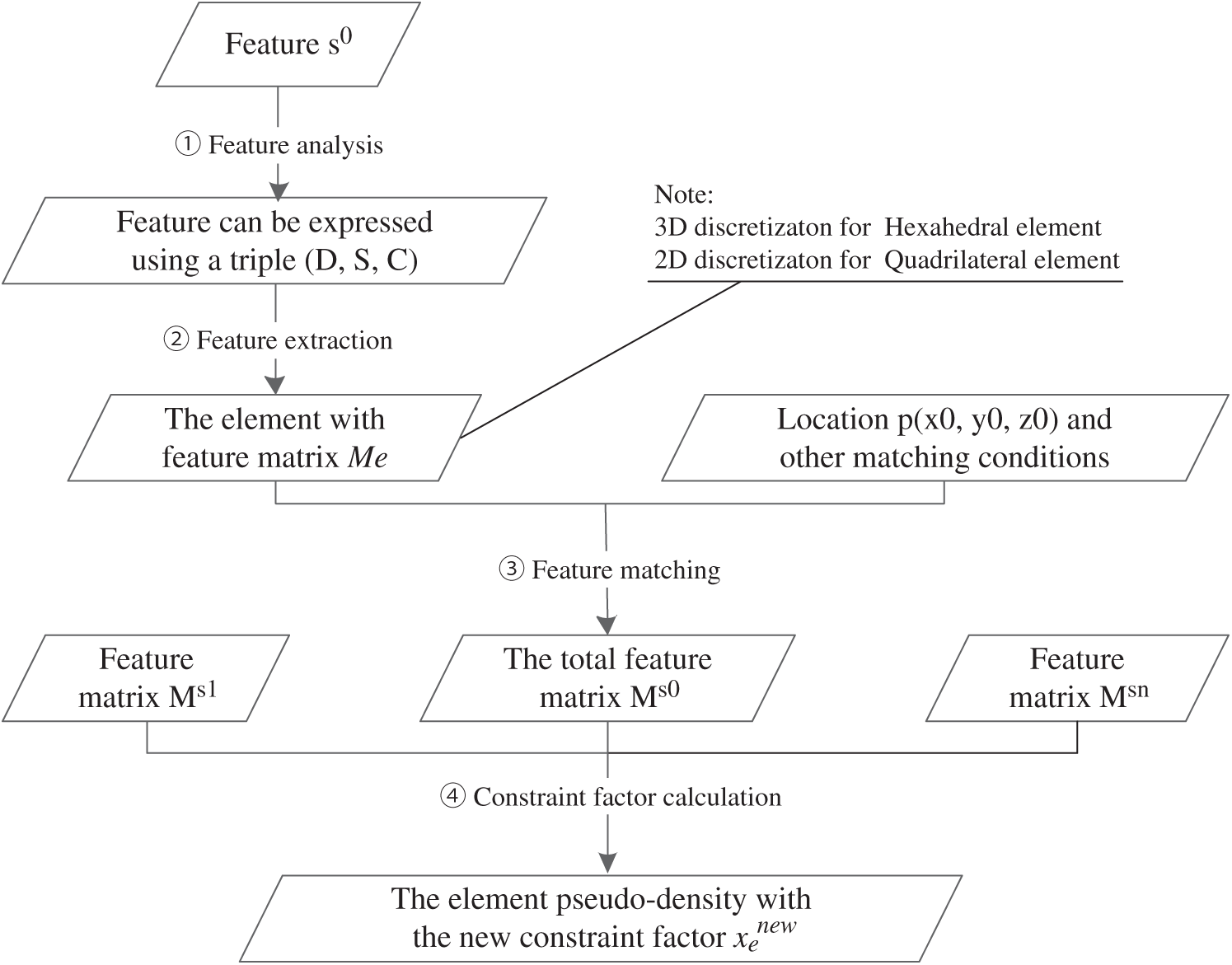
Figure 8: Feature modeling process of feature constraints

Figure 9: Feature-based topology optimization process

5  Numerical Examples

In this section, several 3D structural topology optimization problems with feature constraints are presented to test the performance of the proposed approach. The considered structures are a traditional cantilever beam, a short cantilever beam with double load and a wheel. The aim is to achieve the minimum compliance design of a structure under the prescribed volume constraint, namely the structural design problem is solved under the formulation of the stiffness maximization design.

5.1 A Traditional Cantilever Beam

In the first example, the classical cantilever beam structure is considered to demonstrate the effectiveness of the feature modeling approach. The dimensions of the cantilever beam structure are 60 mm×20 mm×4 mm, as shown in Fig. 10a. Firstly, the feature constraints are not considered in the optimization algorithm, and the optimization result is shown in Fig. 10b. Then, the feature constraint of a circular hole with Φ12×4 mm at (24, 40, 0) is introduced by utilizing the proposed feature modeling approach. The corresponding optimization result is shown in Fig. 10c. It is obvious that there can achieve distinct topology design configuration when the feature modeling approach is employed to enforce the feature constraint compared with that in Fig. 10b. Additionally, the optimization result of a triangular hole constraint is shown in Fig. 10d with use of the feature constraint at a specified location. In many cases, such topological optimization results with feature constraints are more suited to the practical engineering design.

Figure 10: Topology design of a cantilever beam with single load: (a) The physical model; (b) Without feature constraint; (c) With feature constraint of circular hole; (d) With feature constraint of triangular hole

5.2 A Short Cantilever Beam with Double Load

In the second example, a short cantilever beam with double load is considered [35]. The dimensions of the beam structure are 60 mm×60 mm×4 mm, as shown in Fig. 11a. The topology optimization result without feature constraints is shown in Fig. 11b, while the optimization result with feature constraint is shown in Figs. 11c and 11d by enforcing a constraint of circular hole and a constraint of triangular hole at the specified location, respectively. It is seen that the topological designs achieved by employing the proposed approach can meet the requirement of setting holes with specified shapes. There are notably different topology details in the three optimization designs. In the practical engineering application, appropriate optimization results can be used for structural design.

Figure 11: Topology design of a short cantilever beam with double load: (a) The physical model; (b) Without feature constraint; (c) With feature constraint of circular hole; (d) With feature constraint of triangular hole

5.3 Topology Optimization of 3D Wheel

The third example under consideration is the structural design of 3D wheel [35]. The physical model including boundary condition and loading are depicted in Fig. 12a. The specified feature constraint is a triangular hole. The design domain is discretized by a 60×20×20 finite element (FE) mesh. In order to obtain the minimum compliance design of structure with feature constraints, the proposed feature modeling approach is employed. The topology optimization results are shown in Figs. 12b and 12c. Compared with the structural design of Fig. 12b, the optimization result of Fig. 12c can achieve a design with the specified feature constraint of triangular hole. Furthermore, the iterative histories of the objective function for the optimization result in Fig. 12c are presented in Fig. 13. It is seen that there are stable iterations and fast convergence of design optimization, thus the proposed feature modeling approach is effective and efficient to achieve 3D structural topology designs with feature constraints.

Figure 12: Topology design of 3D wheel: (a) The physical model; (b) Without feature constraint; (c) With feature constraint of triangular hole

Figure 13: Iterative histories of the objective function for the optimization result in Fig. 12c

6  Conclusions

In this paper, a feature modeling approach is developed for addressing the 3D structural topology optimization problems with feature constraints. Considering the practical application of optimization results, a feature introduction scheme with constraint factors is proposed. The introduction of the present scheme separates the feature constraint modeling from the core algorithm of topology optimization, and only the constraint factors can realize the loose coupling of the optimization algorithm, which can provide a more convenient extension way for the application of topology optimization. To further improve the feature extraction model, it can lay a foundation for the establishment of constraint feature base, and then provide empirical support based on database for topology optimization, which will open up a new way to promote the application of topology optimization methods. Numerical examples show feasibility and effectiveness of the proposed feature modeling approach.

This paper focuses on the free-form optimization problem with embedded geometric features fixed at certain positions. It should be noted that the location of the embedded features strongly influences the performance of the optimized structure. As a consequence, application of the proposed approach to solve the problem of optimally embedded predesigned objects into a design region and designing the topology of the connecting structure is also of interest. More attention will be drawn to exploring such issues in future.

Acknowledgement: The authors would like to thank very much to the anonymous reviewers for their insightful suggestions and comments on the early version of this paper.

Funding Statement: This work is supported by the National Natural Science Foundation of China (12002218) and the Youth Foundation of Education Department of Liaoning Province (JYT19034). These supports are gratefully acknowledged.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

 1.  Bendsøe, M. P., Kikuchi, N. (1988). Generating optimal topologies in structural design using a homogenization method. Computer Methods in Applied Mechanics and Engineering, 71(2), 197–224. DOI 10.1016/0045-7825(88)90086-2. [Google Scholar] [CrossRef]

 2.  Bendsøe, M. P. (1989). Optimal shape design as a material distribution problem. Structural Optimization, 1(4), 193–202. DOI 10.1007/BF01650949. [Google Scholar] [CrossRef]

 3.  Zhou, M., Rozvany, G. I. N. (1991). The COC algorithm, Part II: Topological, geometry and generalized shape optimization. Computer Methods in Applied Mechanics and Engineering, 89(1–3), 309–336. DOI 10.1016/0045-7825(91)90046-9. [Google Scholar] [CrossRef]

 4.  Bendsøe, M. P., Sigmund, O. (1999). Material interpolation schemes in topology optimization. Archive of Applied Mechanics, 69(9–10), 635–654. DOI 10.1007/s004190050248. [Google Scholar] [CrossRef]

 5.  Xie, Y. M., Steven, G. P. (1993). A simple evolutionary procedure for structural optimization. Computers and Structures, 49(5), 885–896. DOI 10.1016/0045-7949(93)90035-C. [Google Scholar] [CrossRef]

 6.  Huang, X., Xie, Y. M. (2007). Convergent and mesh-independent solutions for the bi-directional evolutionary structural optimization method. Finite Elements in Analysis and Design, 43(14), 1039–1049. DOI 10.1016/j.finel.2007.06.006. [Google Scholar] [CrossRef]

 7.  Wang, M. Y., Wang, X. M., Guo, D. M. (2003). A level set method for structural topology optimization. Computer Methods in Applied Mechanics and Engineering, 192(1–2), 227–246. DOI 10.1016/S0045-7825(02)00559-5. [Google Scholar] [CrossRef]

 8.  Allaire, G., Jouve, F., Toader, A. M. (2004). Structural optimization using sensitivity analysis and a level-set method. Journal of Computational Physics, 194(1), 363–393. DOI 10.1016/j.jcp.2003.09.032. [Google Scholar] [CrossRef]

 9.  Wei, P., Wang, W. W., Yang, Y., Wang, M. Y. (2020). Level set band method: A combination of density-based and level set methods for the topology optimization of continuums. Frontiers of Mechanical Engineering, 15(3), 390–405. DOI 10.1007/s11465-020-0588-0. [Google Scholar] [CrossRef]

10. Zhang, W. S., Yuan, J., Zhang, J., Guo, X. (2016). A new topology optimization approach based on moving morphable components (MMC) and the ersatz material model. Structural and Multidisciplinary Optimization, 53(6), 1243–1260. DOI 10.1007/s00158-015-1372-3. [Google Scholar] [CrossRef]

11. Zhang, W. S., Chen, J. S., Zhu, X. F., Zhou, J. H., Xue, D. C. et al. (2017). Explicit three dimensional topology optimization via moving morphable void (MMV) approach. Computer Methods in Applied Mechanics and Engineering, 322, 590–614. DOI 10.1016/j.cma.2017.05.002. [Google Scholar] [CrossRef]

12. Zhou, Y., Zhang, W. H., Zhu, J. H., Xu, Z. (2016). Feature-driven topology optimization method with signed distance function. Computer Methods in Applied Mechanics and Engineering, 310, 1–32. DOI 10.1016/j.cma.2016.06.027. [Google Scholar] [CrossRef]

13. Bendsøe, M. P., Sigmund, O. (2003). Topology optimization: Theory, methods and applications. Berlin: Springer. [Google Scholar]

14. Eschenauer, H. A., Olhoff, N. (2001). Topology optimization of continuum structures: A review. Applied Mechanics Reviews, 54(4), 331–390. DOI 10.1115/1.1388075. [Google Scholar] [CrossRef]

15. Rozvany, G. I. N. (2009). A critical review of established methods of structural topology optimization. Structural and Multidisciplinary Optimization, 37(3), 217–237. DOI 10.1007/s00158-007-0217-0. [Google Scholar] [CrossRef]

16. Sigmund, O., Maute, K. (2013). Topology optimization approaches. Structural and Multidisciplinary Optimization, 48(6), 1031–1055. DOI 10.1007/s00158-013-0978-6. [Google Scholar] [CrossRef]

17. Deaton, J. D., Grandhi, R. V. (2014). A survey of structural and multidisciplinary continuum topology optimization: Post 2000. Structural and Multidisciplinary Optimization, 49(1), 1–38. DOI 10.1007/s00158-013-0956-z. [Google Scholar] [CrossRef]

18. Wang, Y. J., Wang, Z. P., Xia, Z. H., Poh, L. H. (2018). Structural design optimization using isogeometric analysis: A comprehensive review. Computer Modeling in Engineering & Sciences, 117(3), 455–507. DOI 10.31614/cmes.2018.04603. [Google Scholar] [CrossRef]

19. Wang, Y. J., Liao, Z. Y., Shi, S. Y., Wang, Z. P., Poh, L. H. (2020). Data-driven structural design optimization for petal-shaped auxetics using isogeometric analysis. Computer Modeling in Engineering & Sciences, 122(2), 433–458. DOI 10.32604/cmes.2020.08680. [Google Scholar] [CrossRef]

20. Harzheim, L., Graf, G. (2006). A review of optimization of cast parts using topology optimization. Structural and Multidisciplinary Optimization, 31(5), 388–399. DOI 10.1007/s00158-005-0554-9. [Google Scholar] [CrossRef]

21. Wang, M. Q., Li, Z. D. (2010). Research on method of topology optimization design of continuum structures for manufacturing. China Mechanical Engineering, 21(5), 524–528. DOI 10.3969/j.issn.1004132X(2010)05052405. [Google Scholar] [CrossRef]

22. Qiu, F. S., Pei, Y., Sun, C., Liu, S. T. (2010). Topology optimization design of 3D wing box. Computer Integrated Manufacturing Systems, 16(11), 2405–2409. DOI 10.13196/j.cims.2010.11.87.qiufsh.009. [Google Scholar] [CrossRef]

23. Qiu, F. S., Ji, W. Q., Xu, H. C. (2013). The vertical tail of topology optimization design study based on improved variable density method. Journal of Shenyang Aerospace University, 30(1), 26–29. DOI 10.3969/j.issn.2095-1248.2013.01.006. [Google Scholar] [CrossRef]

24. Liu, J. K., Ma, Y. S. (2016). A survey of manufacturing oriented topology optimization methods. Advances in Engineering Software, 100, 161–175. DOI 10.1016/j.advengsoft.2016.07.017. [Google Scholar] [CrossRef]

25. Wang, X., Hu, P., Kang, Z. (2020). Layout optimization of continuum structures embedded with movable components and holes simultaneously. Structural and Multidiplinary Optimization, 61(4), 1757. DOI 10.1007/s00158-019-02463-9. [Google Scholar] [CrossRef]

26. Jiu, L. P., Zhang, W. H., Meng, L., Zhou, Y., Chen, L. (2020). A CAD-oriented structural topology optimization method. Computers and Structures, 239, 106324. DOI 10.1016/j.compstruc.2020.106324. [Google Scholar] [CrossRef]

27. Vatanabe, S. L., Lippi, T. N., Lima, C. R. D., Paulino, G. H., Silva, E. C. N. (2016). Topology optimization with manufacturing constraints: A unified projection-based approach. Advances in Engineering Software, 100, 97–112. DOI 10.1016/j.advengsoft.2016.07.002. [Google Scholar] [CrossRef]

28. Chen, F., Chen, B. S., Zhou, D. W., Zhang, S. (2016). Research and software implementation of variable connection algorithm for structural topology optimization. Chinese Journal of Computational Mechanics, 33(2), 158–164. DOI 10.7511/jslx201602004. [Google Scholar] [CrossRef]

29. Sørensen, S. N., Lund, E. (2013). Topology and thickness optimization of laminated composites including manufacturing constraints. Structural and Multidisciplinary Optimization, 48(2), 249–265. DOI 10.1007/s00158-013-0904-y. [Google Scholar] [CrossRef]

30. Du, Y. X., Fu, J. J., Tian, Q. H. (2011). Topology optimization for mid-bed of a CNC gear shaping machine tool based on manufacturing constraints. Journal of Engineering Design, 18(5), 341–340. DOI 10.3785/j.issn.1006.754X.2011.05.005. [Google Scholar] [CrossRef]

31. Liu, S. T., Li, Q. H., Chen, W. J., Tong, L. Y., Cheng, G. D. (2015). An identification method for enclosed voids restriction in manufacturability design for additive manufacturing structures. Frontiers of Mechanical Engineering, 10(2), 126–137. DOI 10.1007/s11465-015-0340-3. [Google Scholar] [CrossRef]

32. Zhang, W. H., Zhou, Y., Zhu, J. H. (2017). A comprehensive study of feature definitions with solids and voids for topology optimization. Computer Methods in Applied Mechanics and Engineering, 325, 289–313. DOI 10.1016/j.cma.2017.07.004. [Google Scholar] [CrossRef]

33. Zhu, J. H., Zhao, Y. B., Zhang, W. H., Gu, X. J., Gao, T. et al. (2019). Bio-inspired feature-driven topology optimization for rudder structure design. Engineered Science, 5, 46–55. DOI 10.30919/es8d716. [Google Scholar] [CrossRef]

34. Xu, Z., Zhang, W. H., Zhou, Y., Zhu, J. H. (2020). Multiscale topology optimization using feature-driven method. Chinese Journal of Aeronautics, 2(2), 621–633. DOI 10.1016/j.cja.2019.07.009. [Google Scholar] [CrossRef]

35. Liu, K., Tovar, A. (2014). An efficient 3D topology optimization code written in Matlab. Structural and Multidisciplinary Optimization, 50(6), 1175–1196. DOI 10.1007/s00158-014-1107-x. [Google Scholar] [CrossRef]

This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.