Computer Modeling in Engineering & Sciences

DOI: 10.32604/cmes.2021.013077

ARTICLE

Nonlinear Thermal Buoyancy on Ferromagnetic Liquid Stream Over a Radiated Elastic Surface with Non Fourier Heat Flux

T. K. Sreelakshmi1, Abraham Annamma1, A. S. Chethan1, M. Krishna Murthy2 and C. S. K. Raju3,*

1Department of Mathematics, BMS Institute of Technology and Management, Bengaluru, 560064, India
2Department of Mathematics, School of Applied Sciences, REVA University, Bengaluru, 560064, India
3Department of Mathematics, GITAM School of Science, GITAM Deemed to be University, Bengaluru, 562163, India
*Corresponding Author: C. S. K. Raju. Email: sivaphd90@gmail.com
Received: 24 July 2020; Accepted: 30 October 2020

1  Introduction

Nowadays, the energy equation with Fourier’s law is parabolic. It demonstrates that the complete system is instantaneously influenced by the initial disruptions. This difficulty has been measured through consideration of thermal relaxation time in Fourier’s law. Environmental hollows and closed vessels with heated walls are the best examples of non-Fourier flux. Additional in the convection flows connected with heat-denunciation structures for a long period of intense sea power divisions where the sea environment is stratified. Flows with non-Fourier flux are of ample significance in several elastic flow configurations including geothermal systems, geological transport, Lake Thermohydraulics, volcanic flows, power plant condensation system, etc. This phenomenon important because of nonlinear thermal differences, which gives upsurge to a density discrepancy in the medium. It has significance in dissimilar normal processes, for example, transportation forms in the marine where non-Fourier flux exists since of salinity deviation. Furthermore, the temperature variance changes from layer to layer and such kinds of movements have wide demands in oceanography, industry and agriculture processes. The boundary layer of non-Newtonian liquids may be a current subject of exploration for the insistent pros since of their various industrial, design and manufacturing significance. Diverse progressed liquids connect paints, zams, toothpaste and slurries. The developments of these liquids essentially look into entirely specific approaches for example, glass blowing, design of aerospace particles and ceaseless casting and so on. The stretching out gives a unidirectional prologue to the extrudate along these lines moving forward its liquid mechanical properties. By the benefit of this many researchers have investigated the flow of non-Newtonian fluid with non-Fourier flux. Few of them are, Zubair et al. [1,2] developed simulation of nonlinear convective thixotropic liquid with Cattaneo–Christov heat flux and Stagnation point flow of third-grade liquid due to variable thickness a useful application to non-Fourier heat flux approach. A Double-diffusion model for viscoelastic nanofluid with activation energy and nonlinear thermal radiation was studied by Muhammad et al. [3]. Nadeem et al. [4,5] discovered Roseland analysis for ferromagnetic fluid in presence of gyrotactic microorganisms and magnetic dipole and Darcy–Forchheimer flow under rotating disk and entropy generation with thermal radiation and heat source/sink. Ijaz et al. [6,7] investigated the Simulation of the magnetic dipole on gyrotactic ferromagnetic fluid flow with nonlinear thermal radiation and Arrhenius activation energy and Joule heating for Walter fluid with Cattaneo–Christov double diffusion model. Structure of head-to-head domain wall in cylindrical amorphous ferromagnetic microwire and a method of anisotropy coefficient estimation were founded by Mikhail et al. [8]. Misra et al. [9] reported on temperature distribution and entropy generation during Darcy–Forchheimer–Brinkman electrokinetic flow in a microfluidic tube subject to a prescribed heat flux. Ferdows et al. [10] analyzed dual solutions for boundary layer flow and heat transfer of biomagnetic fluid over a stretching/shrinking sheet in presence of a magnetic dipole and a prescribed heat flux. Sankar Giri et al. [11] portrayed homogeneous heterogeneous reaction mechanisms on MHD carbon nanotube flow over a stretching cylinder with prescribed heat flux using differential transform method. Anupam et al. [12] analyzed optimization of heat transfer properties on ferrofluid flow over a stretching sheet in the presence of static magnetic field. Hydrodynamic and heat transfer properties of magnetic fluid in porous medium considering nanoparticle shapes and magnetic field dependent viscosity studied by Izadi et al. [13]. Nadeem et al. [14] investigated on a computational model for suspensions of motile micro- organisms in the flow of ferrofluid. Lucas et al. [15] analyzed a numerical study on heat transfer of a ferrofluid flow in a square cavity under simultaneous gravitational and magnetic convection. Some of the researchers are analyzing ferrofluids in different geometric ways [16–21].

Recently, the nonlinear temperature-density association in which the flow is obsessed by buoyancy may utilize a durable impact on the heat transfer physiognomies. It has numerous practical importance in geothermal, bio-physics, bio-thermal, astrophysics, geophysics and engineering processes; for example, the residual warm water discharged from a geothermal power plant is generally prepared off from shafts over subsurface reinjection. By this many authors started implementing the nonlinear buoyancy forces in the flow. The nonlinear convection with insulating boundaries was initiated by Busse et al. [22]. Later on, Shi et al. [23] nonlinear diffusion convection equation is solved by using the Lattice Boltzmann method. Stagnation point flow over shrinking porous surface with nonlinear convection is solved numerically by Kumar et al. [24]. Very recently, the authors considered the nonlinear thermal and diffusion buoyancy forces and magnetic field effects on non-Newtonian, micro and nanofluid is investigated by the authors [25–29] and found that the nonlinear convection made significant changes in the flow.

The prime idea of the current assessment is to explain the centrality of explores the stream and heat transfer of ferromagnetic liquid over an elastic surface with radiation and non-Fourier heat flux. The governing equations identified with our examination are changed into non-linear ODE’s by utilizing fitting likeness transformations, which are at that point fathomed by Runge–Kutta besides shooting procedure. Empower, the impacts of assorted non-dimensional physical parameters on speed and temperature profiles are delineated graphically. The variety of Skin grinding and local Nusselt number for both PWT and PHF cases for distinctive assessment of non-dimensional parameters have been classified.

2  Mathematical Formulation

We assess the consistent two-dimensional an incompressible ferromagnetic liquid driven by an emanated flexible surface with non-Fourier heat flux as appeared in Fig. 1. Here we have considered the Cartesian arrange framework with settled beginning such that the x-axis is along the direction of the stretched surface and the y-axis is taken ordinarily to the sheet. The sheet is extended with a speed u(x) = cx which is corresponding to the distance from the origin, slanted at a point 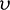with the horizontal. We have moreover expected that the liquids as an ambient temperature 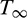and 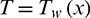as temperature of the surface. To amplify the heat transfer rate we considered the thermal radiation and Cattaneo–Christov heat flux. The joule heating and viscous dissipation are neglected due to flux conditions at the surface.

Figure 1: Physical model of the problem

The governing boundary layer equations beneath the over-specified suspicious are as follows:

The conservation of mass equation, the momentum equation, and the energy equation are:

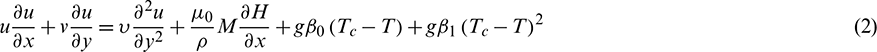
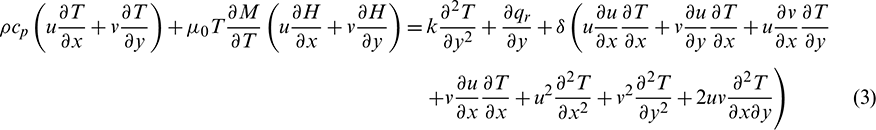
The limit conditions for fathoming the above governing equations for both the Prescribed Wall Temperature (PWT) and Prescribed Heat Flux (PHF) are:

Here A and D are positive constants, and 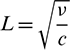is the characteristic length. The stream of ferrofluid is influenced by the magnetic field due to the magnetic dipole whose magnetic scalar potential is given by

where is the magnetic field quality of the source. The components of the magnetic field H are

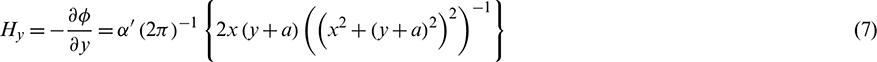
Since the magnetic body drive is proportional to the gradient of the magnitude H, we get

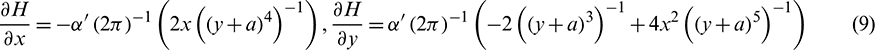
Variation of magnetization M with temperature T is approximated by a linear equation

where K is the paramagnetic coefficient.

3  Solution Procedure of the Problem

We presently present the non-dimensional factors as expected by Anderson [21]

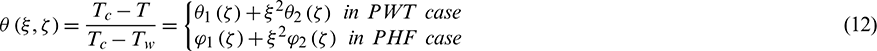
where 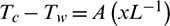in PST case,

in the PHF case.

Radiative heat flux is

By considering Eq. (13) the energy Eq. (3) takes the form

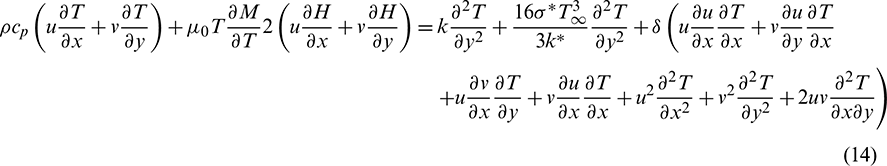
The limit conditions are taken from (4) as follows:

Presenting the stream function 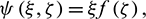that fulfills the conservation of mass equation within the dimensionless frame, we get

where the prime indicates differentiation concerning utilizing Eqs. (9)–(13) and (16) in (1), (2), (14), and (4) we get the taking after limit value problem with boundary conditions.

3.1 Prescribed Wall Temperature (PWT)

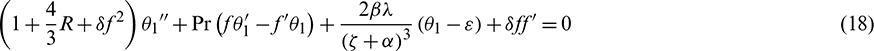
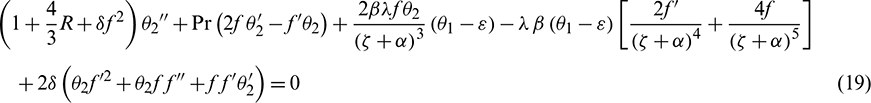
Limit conditions are:

3.2 Prescribe Heat Flux (PHF)

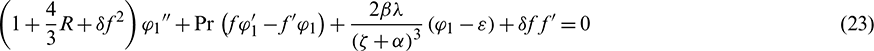
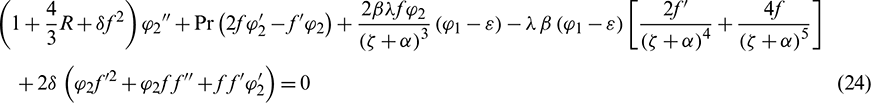
Limit conditions are:

The dimensionless parameters, which show up unequivocally within the transformed problem, are the viscous dissipation parameter 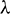, the dimensionless Curie temperature 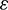, the ferrohydrodynamic interaction parameter 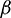, the nonlinear convention parameter 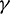, the radiation parameter R, the non-Fourier heat flux 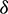and the dimensionless distance 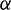from the starting to the center of the attractive shaft, characterized independently as

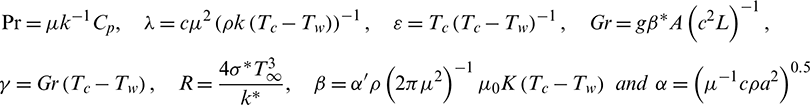
Eqs. (17)–(21) and (22)–(26) constitute two sets of nonlinear, two-point boundary esteem issues. Trial values 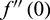, , 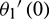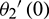and 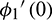, 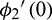are balanced iteratively by Newton–Raphson’s strategy to guarantee a quadratic merging of the iterative trial values required in arrange to satisfy the external boundary conditions.

In this study, the physical parameters of intrigued are skin friction cf and local Nusselt number Nux which are characterized as follows:

where 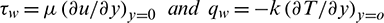are shear stress and heat flux at the sheet, respectively. By utilizing non-dimensional similarity changes (16), we get

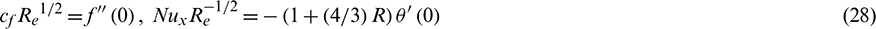
Tab. 1 is organized to examine the impact of the before said parameters on the skin friction coefficient and Nusselt number.

Table 1: The variations of friction factor and local Nusselt number for distinct estimations of non-dimensional governing parameters for both the PHF and PWT cases

4  Method of Solution

The nonlinear ordinary differential equations and boundary conditions for two cases PWT for (17)–(21) and PHF for (22)–(26) are solved numerically using Runge–Kutta shooting method. Initially, the set of nonlinear ordinary differential equations converted into first order differential equations, by using the following process:

PWT case: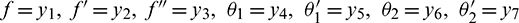

PHF case: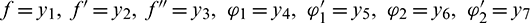

4.1 Prescribed Wall Temperature (PWT)

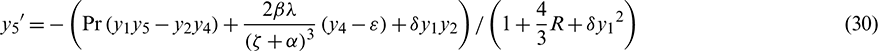
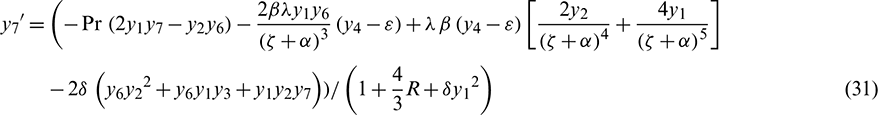
Limit conditions are:

4.2 Prescribe Heat Flux (PHF)

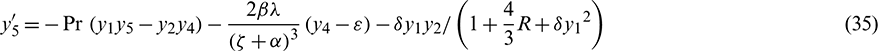
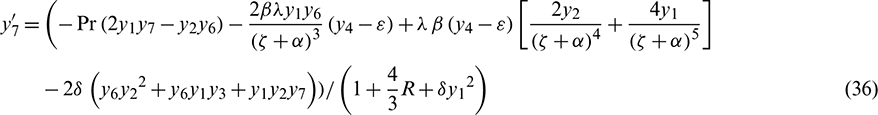
Limit conditions are:

Eqs. (29)–(38) are integrated by taking the help of Runge–Kutta shooting method with the successive iterative step length 0.01.

5  Results and Discussion

If we observe the Eqs. (17)–(24) are highly nonlinear with coupling nature. So, it is very difficult to solve by using the analytical technique. Due to this, we used Numerical methods to solve the modelled governing system. The current article is to investigate the nonlinear thermal buoyancy on ferromagnetic liquid over a radiated elastic surface with non-Fourier heat flux. Nondimensional governing Eqs. (17)–(19), (22)–(24) with the limit conditions (20), (21), (25) and (26) were illuminated numerically with R-K shooting method. So as to explore the comes about, numerical calculations are completed by considering various estimations of non-dimensional governing parameters 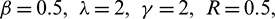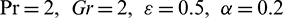these values are considered as settled all through the barring the assortments within the separate figures and tables. In figures solid line illustrates prescribed heat flux (PHF) case and dashed lines refer to prescribed wall temperature (PWT) case. Figs. 2 and 3 outline the influence of radiation on temperature and velocity profiles. It is seen that the impact of radiation is showing mixed behavior in both temperature and velocity profiles for PHF and PWT cases. Physically, as raising values of thermal radiation generate heat molecules in the flow, but, whereas the non-Fourier flux has dominated. This causes to show mixed behavior in the presence of radiation.

Figure 2: The temperature with impacts of radiation

Figure 3: Impacts of radiation on velocity

Figs. 4 and 5 show up the coordinated effort of the ferrohydrodynamic parameter 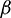which makes strides temperature profile in PHF case and lessens in PWT case. As 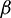extends, the nearness of the attractive field actuated by the attractive dipole on the liquid goes roughly as a hindering force, along these lines reducing the axial speed which achieves smoothing 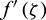. Figs. 6 and 7 noted that the temperature and velocity profiles in the presence of the viscous dissipation parameter 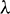. It is seen that the temperature profile is eternally outspreading with an improvement 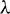in two cases of the flow (PWT and PHF). As bigger values 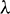give rise to more dissipation among the particles, this helps to improve the thermal boundary layer. But interestingly we observed mixed behavior of the flow in two cases. Figs. 8 and 9 describe the development of velocity and temperature as Gr increments in both the prescribed wall temperature (PWT) and prescribed heat flux (PHF) cases. Gr approximates the proportion of buoyancy constrains to the viscous force following up on the liquid, it also features the centrality of convection in controlling the axial speed. Gr enhances the momentum boundary layer thickness increments endowing the liquid to surface transparently. The advanced buoyancy force tends to the cooling of the slanted broadening sheet acts like an ideal weight slope quickening the liquid inside the boundary layer area. Genuinely suggests heating of the liquid or cooling of the boundary surface. Increment inside the estimation of Gr brings nearly lessening of the thermal boundary layer related with an augmentation inside the wall temperature gradient and in this way making an extension in the heat move rate.

Figure 4: Impacts of ferrohydrodynamic interaction on temperature

Figure 5: Impacts of Ferrohydrodynamic interaction on speed

Figure 6: Impacts of viscous dissipation on temperature

Figure 7: Impacts of viscous dissipation on speed

Figure 8: The temperature with impacts of Grashof number

Figure 9: Impacts of Grashof number on speed

Figs. 10 and 11 appears the impacts of nonlinear convention parameter 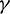on the profiles of temperature and velocity respectively. It is seen that nonlinear convention parameter improves the momentum boundary, whereas temperature has shown mixed behavior. As, we expected raising values of nonlinear convection parameter improves the nonlinearity near the surface, after some time due to the dominance of non-Fourier flux we saw an enhancement in the thermal boundary layer. Figs. 12 and 13 portray the impact of non-Fourier heat flux 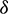which depreciates both the velocity and temperature profiles in PHF case and increments in PWT case. This happens due to dominance of flux and nonlinear convection in the flow, but wall temperature conditions have not created much flux at the surface due to this we saw an increment in profiles of the flow. Figs. 14 and 15 highlights the affect of dimensionless curie parameter which grows temperature and velocity profiles for both PWT and PHF cases. This diminishes the thermal boundary layer thickness near the surface, afterward in the thermal layer is enhanced in PWT case. But, a similar opposite trend is observed in the momentum boundary due to the dominance of flux at the surface mixed performance observed in the flow.

Figure 10: Impacts of nonlinear convection parameters on temperature

Figure 11: Impacts of nonlinear convection parameter on velocity

Figure 12: Impacts of thermal relaxation on temperature

Figure 13: The velocity with impacts of thermal relaxation

Figure 14: Impacts of the dimensionless Curie temperature on temperature

Figure 15: Impacts of the dimensionless Curie temperature on velocity

Tab. 1 displays the impact of the skin friction coefficient and Nusselt number for both the prescribed wall temperature and prescribed heat flux cases of the flow. From this, it is clear that the skin friction coefficient is enhanced with the improved values of 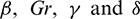and interestingly found that the friction at the surface is very high in prescribed wall temperature case compared to prescribed heat flux. Similarly, the local Nusselt number is encouraged with improving values 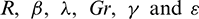. From this study, we found that the flux and wall temperature conditions are useful in automated heating and cooling applications. Tab. 2 is presented to validate my work compared with already existing work under limited situations and the present results are correlated with existing work. It helps me to do a further continuation of the present model.

Table 2: The validation of present results with already available literature under limited case

6  Conclusion

In the current examination, we considered Radiative elastic surface with non-Fourier heat flux on ferromagnetic liquid. Existing PDE’s is changed to ODE’s with the bolster of normal related changes. Subsequently, the higher nonlinear ordinary differential equations are unraveled numerically through R-K and shooting strategy. The computational outcomes for Non-dimensional temperature and speed distributions are offered through outlines. Besides, the numerical estimations of friction factor and Nusselt number are sorted out numerically for distinct physical parameters are acquired. The features of this examination are

1.    The friction factor coefficient is higher in PWT case compared to PHF case. This result helps to conclude that the flux conditions are useful for cooling applications.

2.    The ferromagnet to the hydrodynamic parameter 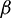can be viably utilized to have a perfect temperature that moves forward the properties of the elastic surface. Since it increases both the friction factor and Nusselt number of the flow.

3.    The thermal relaxation parameter improves the velocity in PWT case and reduces the PHF case. This happens due to flux conditions at the surface, this condition dominates the profiles of the flow.

4.    The nonlinear convection parameter shows mixed performance in velocity and temperature profiles of the PHF case, whereas improvement in PWT case.

Funding Statement: The author(s) received no specific funding for this study.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

 1.  Zubair, M., Waqas, M., Hayat, T., Ayub, M., Alsaedi, A. (2018). Simulation of nonlinear convective thixotropic liquid with Cattaneo–Christov heat flux. Journal of Results in Physics, 8, 1023– 1027. DOI 10.1016/j.rinp.2017.12.016. [Google Scholar] [CrossRef]

 2.  Zubair, M., Waqas, M., Hayat, T., Alsaedi, A., Ayub, M. (2018). Stagnation point flow of third grade liquid due to variable thickness: A useful application to non-Fourier heat flux approach. Results in Physics, 8, 1010–1016. DOI 10.1016/j.rinp.2017.12.010. [Google Scholar] [CrossRef]

 3.  Muhammad, A., Muhammad, Y. M., Misbah, I., Marei, S. A., Ali, S. A. (2019). Double–diffusion model for viscoelastic nanofluid with activation energy and nonlinear thermal radiation. Multidiscipline Modeling in Material and Structures, 16, 93–120. DOI 10.1108/MMMS-03-2019-0046. [Google Scholar] [CrossRef]

 4.  Nadeem, S., Ijaz, M., El-Kott, A., Ayub, M. (2020). Rosseland analysis for ferromagnetic fluid in presence of gyrotactic microorganisms and magnetic dipole. Ain Shams Engineering Journal, (in press). [Google Scholar]

 5.  Naddem, S., Ijaz, M., Ayub, M. (2020). Darcy–Forchheimer flow under rotating disk and entropy generation with thermal radiation and heat source/sink. Journal of Thermal Analysis and Calorimetry, DOI 10.1007/s10973-020-09737-1. [Google Scholar] [CrossRef]

 6.  Ijaz, M., Nadeem, S., Ayub, M. (2020). Simulation of magnetic dipole on gyrotactic ferromagnetic fluid flow with nonlinear thermal radiation. Journal of Thermal Analysis and Calorimetry, DOI 10.1007/s10973-020-09856-9. [Google Scholar] [CrossRef]

 7.  Ijaz, M., Yousaf, M., El Shafey, A. M. (2020). Arrhenius activation energy and Joule heating for Walter fluid with Cattaneo–Christov double–diffusion model. Journal of Thermal Analysis and Calorimetry, 1–12. DOI 10.1007/s10973-020-09270-1. [Google Scholar] [CrossRef]

 8.  Mikhail, V., Irina, B., Sergey, L., Rodionova, V. (2020). Structure of head-to-head domain wall in cylindrical amorphous ferromagnetic microwire and a method of anisotropy coefficient estimation. Journal of Magnetism and Magnetic Materials, 504, 166646. [Google Scholar]

 9.  Misra, J. C., Mallick, B., Steinmann, P. (2020). Temperature distribution and entropy generation during Darcy–Forchheimer–Brinkman electrokinetic flow in a microfluidic tube subject to a prescribed heat flux. Meccanica, 55(5), 1079–1098. DOI 10.1007/s11012-020-01152-y. [Google Scholar] [CrossRef]

10. Ferdows, M., Murtaza, M. G., Misra, J. C., Tzirtzilakis, E. E., Alzahrani, F. (2020). Analyzed dual solutions for boundary layer flow and heat transfer of biomagnetic fluid over a stretching/shrinking sheet in presence of a magnetic dipole and a prescribed heat flux. International Journal of Applied Electromagnetics and Mechanics, 1–17, In press. [Google Scholar]

11. Sankar Giri, S., Das, K., Kundu, P. K. (2020). Homogeneous–heterogeneous reaction mechanism on MHD carbon nanotube flow over a stretching cylinder with prescribed heat flux using differential transform method. Journal of Computational Design and Engineering, 7(3), 337–351. DOI 10.1093/jcde/qwaa028. [Google Scholar] [CrossRef]

12. Anupam, B., Akmal, H. (2020). Optimization of heat transfer properties on ferrofluid flow over a stretching sheet in the presence of static magnetic field. Journal of Thermal Analysis and Calorimetry, 1–18. DOI 10.1007/s10973-020-09636-5. [Google Scholar] [CrossRef]

13. Izadi, M., Javanahram, M., Zadeh, S. M. H., Jing, D. (2020). Hydrodynamic and heat transfer properties of magnetic fluid in porous medium considering nanoparticle shapes and magnetic field dependent viscosity. Chinese Journal of Chemical Engineering, 28(2), 329–339. DOI 10.1016/j.cjche.2019.04.024. [Google Scholar] [CrossRef]

14. Nadeem, S., Alblawi, A., Muhammad, N., Alarifi, I. M., Issakhov, A. et al. (2020). A computational model for suspensions of motile micro- organisms in the flow of ferrofluid. Journal of Molecular Liquids, 298, 112033. DOI 10.1016/j.molliq.2019.112033. [Google Scholar] [CrossRef]

15. Lucas, H. P. C., Ivan, R. S., Arthur, A. R. C., Adriano, P. R., Taygoara, F. O. (2020). A numerical study on heat transfer of a ferrofluid flow in a square cavity under simultaneous gravitational and magnetic convection. Theoretical Computational Fluid Dynamics, 34, 119–132. [Google Scholar]

16. Hui, Z., Yugang, Z., Wenzhen, F., Chaoyang, Z., Fangqi, Z. et al. (2020). Active control of the freezing process of a ferrofluid droplet with magnetic fields. Applied Thermal Engineering, 176, 115444. [Google Scholar]

17. Abazar, A., Mohammad, S., Mehdi, A., Mahdi, P., Mohammad, P. et al. (2020). Experimental characterization of magnetic field effects on heat transfer coefficient and pressure drop for a ferrofluid flow in a circular tube. Journal of Molecular Liquids, 299, 112206. [Google Scholar]

18. Bijarchi, M. A., Favakeh, A., Shafii, M. B. (2020). The effect of a non-uniform pulse-width modulated magnetic field with different angles on the swinging ferrofluid droplet formation. Journal of Industrial and Engineering Chemistry, 84, 106–119. DOI 10.1016/j.jiec.2019.12.026. [Google Scholar] [CrossRef]

19. Pouya, B., Davood, T., Arash, K. (2020). Application of rotating circular obstacles in improving ferrofluid heat transfer in an enclosure saturated with porous medium subjected to a magnetic field. Journal of Thermal Analysis and Calorimetry, 37, 1–23. [Google Scholar]

20. Acharya, N. (2020). Framing the impacts of highly oscillating magnetic field on the ferrofluid flow over a spinning disk considering nanoparticle diameter and solid–liquid interfacial layer. Journal of Heat Transfer, 142(10), 263. DOI 10.1115/1.4047503. [Google Scholar] [CrossRef]

21. Andersson, H. I. (2002). Slip flow past a stretching surface. Acta Mechanica, 158(1–2), 121–125. DOI 10.1007/BF01463174. [Google Scholar] [CrossRef]

22. Busse, F. H., Riahi, N. (1980). Nonlinear convection in a layer with nearly insulating boundaries. Journal of Fluid Mechanics, 96(2), 243–256. DOI 10.1017/S0022112080002091. [Google Scholar] [CrossRef]

23. Shi, B., Guo, Z. (2009). Lattice Boltzmann model for nonlinear convection-diffusion equations. Physical Review E, 79(1), 195. DOI 10.1103/PhysRevE.79.016701. [Google Scholar] [CrossRef]

24. Kumar, R., Sood, S. (2017). Numerical analysis of stagnation point nonlinear convection flow through porous medium over a shrinking sheet. International Journal of Applied and Computational Mathematics, 3(2), 971–985. DOI 10.1007/s40819-016-0150-2. [Google Scholar] [CrossRef]

25. Upadhya, S. M., SureshKumar Raju, S., Raju, C. S. K., Chokri, M. (2020). Arrhenius activation and zero mass flux conditions on nonlinear convective jeffrey fluid over an electrically conducting and radiated sheet. Arabian Journal for Science and Engineering, 340(4), 68. DOI 10.1007/s13369-020-04687-0. [Google Scholar] [CrossRef]

26. Zemedu, C., Wubshet, I. (2020). Nonlinear convection flow of micropolar nanofluid due to a rotating disk with multiple slip flow. Mathematical Problems in Engineering, 2020(3), 1–19. DOI 10.1155/2020/4735650. [Google Scholar] [CrossRef]

27. Upadhya, S. M., Renuka Devi, R. L. V., Raju, C. S. K., Hafiz, M. A. (2020). Magnetohydrodynamic nonlinear thermal convection nanofluid flow over a radiated porous rotating disk with internal heating, 1–12. DOI 10.1007/s10973-020-09669-w. [Google Scholar] [CrossRef]

28. Kiran, P., Bhadauria, B. S., Roslan, R. (2020). The effect of throughflow on weakly nonlinear convection in a viscoelastic saturated porous medium. Journal of Nanofluids, 9(1), 36–46. DOI 10.1166/jon.2020.1724. [Google Scholar] [CrossRef]

29. Upadhya, S. M., Raju, C. S. K., Saleem, S., Alderremy, A. A. (2018). Modified Fourier heat flux on MHD flow over stretched cylinder filled with dust, graphene and silver nanoparticles. Results in Physics, 9, 1377–1385. DOI 10.1016/j.rinp.2018.04.038. [Google Scholar] [CrossRef]

30. Chen, C. H. (1998). Laminar mixed convection adjacent to vertical continuously stretching sheets. Heat and Mass Transfer, 33(5–6), 471–476. DOI 10.1007/s002310050217. [Google Scholar] [CrossRef]

This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.